Calculer la distance entre deux points - Exercice 2

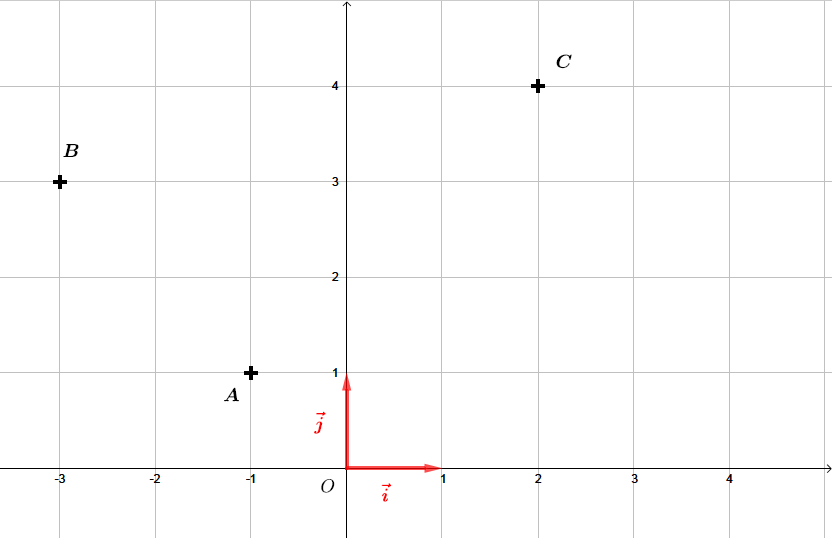
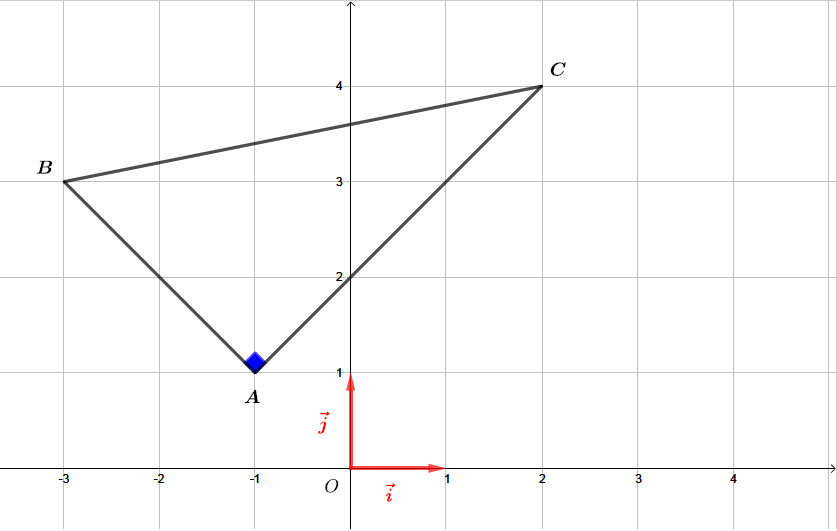
Calculons les longueurs des trois côtés du triangle $$ABC$$.
Ainsi :
$$AB=\sqrt{\left(x_{B} -x_{A} \right)^{2} +\left(y_{B} -y_{A} \right)^{2} }\Leftrightarrow AB=\sqrt{\left(-3-\left(-1\right)\right)^{2} +\left(3-1\right)^{2} } \Leftrightarrow AB=\sqrt{\left(-2\right)^{2} +2^{2} }$$
D'où :
$$AC=\sqrt{\left(x_{C} -x_{A} \right)^{2} +\left(y_{C} -y_{A} \right)^{2} }\Leftrightarrow AC=\sqrt{\left(2-\left(-1\right)\right)^{2} +\left(4-1\right)^{2} } \Leftrightarrow AC=\sqrt{3^{2} +3^{2} }$$
D'où :
$$BC=\sqrt{\left(x_{C} -x_{B} \right)^{2} +\left(y_{C} -y_{B} \right)^{2} }\Leftrightarrow BC=\sqrt{\left(2-\left(-3\right)\right)^{2} +\left(4-3\right)^{2} } \Leftrightarrow BC=\sqrt{5^{2} +1^{2} }$$
D'où :
$$\red{\text{D'une part :}}$$ $$BC^{2}=\left(\sqrt{26}\right)^{2}=26$$
$$\red{\text{D'autre part :}}$$ $$AC^{2}+AB^{2}=\left(\sqrt{18}\right)^{2}+\left(\sqrt{8}\right)^{2}$$ ainsi : $$AC^{2}+AB^{2}=18+8=26$$
Il en résulte donc que :
$$BC^{2} =AB^{2} +AC^{2}$$ alors, d’après la réciproque du théorème de Pythagore, le triangle $$ABC$$ est rectangle en $$A$$.