Les suites
Exercice 7 - Exercice 1
1 min
0
Des Suites avec des exponentielles :)
Question 1
Le but de l’exercice est démontrer que l’équation :
admet une unique solution dans l’ensemble des nombres réels, et de construire une suite qui converge vers cette unique solution.
On note la fonction définie sur par :
admet une unique solution dans l’ensemble des nombres réels, et de construire une suite qui converge vers cette unique solution.
On note la fonction définie sur par :
Démontrer que si est solution de l’équation alors .
Correction
: équivaut successivement à :
Nous avons démontré que si est solution de l’équation alors .
Nous avons démontré que si est solution de l’équation alors .
Question 2
Calculer la limite de en .
Correction
Ici, il s'agit d'une limite par composition.
On commence par calculer .
On pose .
Ainsi : .
Par composition :
Finalement :
On commence par calculer .
On pose .
Ainsi : .
Par composition :
Finalement :
Question 3
Calculer la limite de en .
Correction
Ici, il s'agit d'une limite par composition.
On commence par calculer .
On pose .
Ainsi : .
Par composition :
Finalement :
On commence par calculer .
On pose .
Ainsi : .
Par composition :
Finalement :
Question 4
Étudier le sens de variations de la fonction sur .
Correction
Soit .
est dérivable sur .
Pour tout , on sait que .
De ce fait, pour tout , on a : ce qui implique que la fonction est strictement croissante sur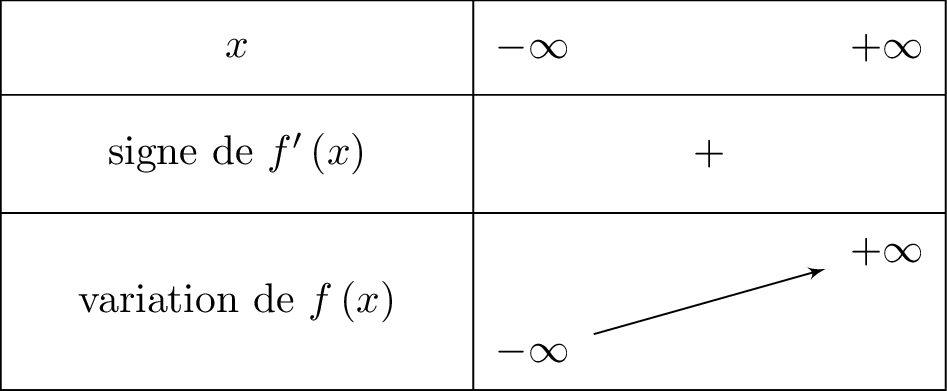
est dérivable sur .
Pour tout , on sait que .
De ce fait, pour tout , on a : ce qui implique que la fonction est strictement croissante sur

Question 5
En déduire que l’équation possède une unique solution sur , notée .
Correction
D'après la question , nous avons démontré que si est solution de l’équation alors .
Nous pouvons donc traduire la question par : démontrer que l'équation admet une unique solution sur , notée .
Sur , la fonction est continue et strictement croissante.
De plus, et . Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution appartenant à tel que . 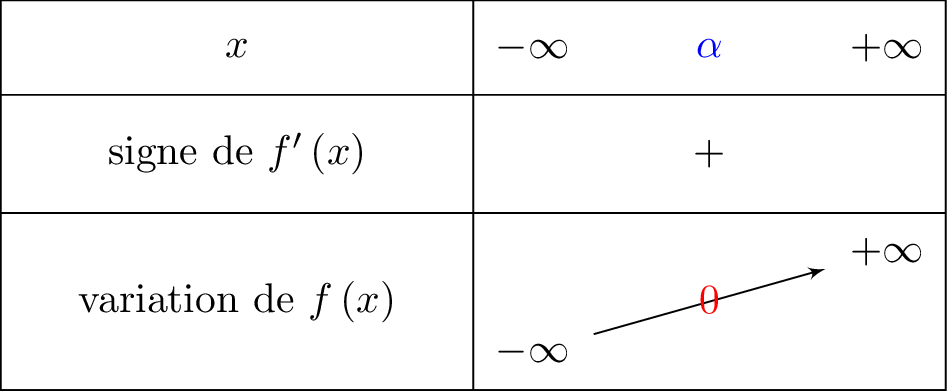
Nous pouvons donc traduire la question par : démontrer que l'équation admet une unique solution sur , notée .
De plus, et . Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution appartenant à tel que .
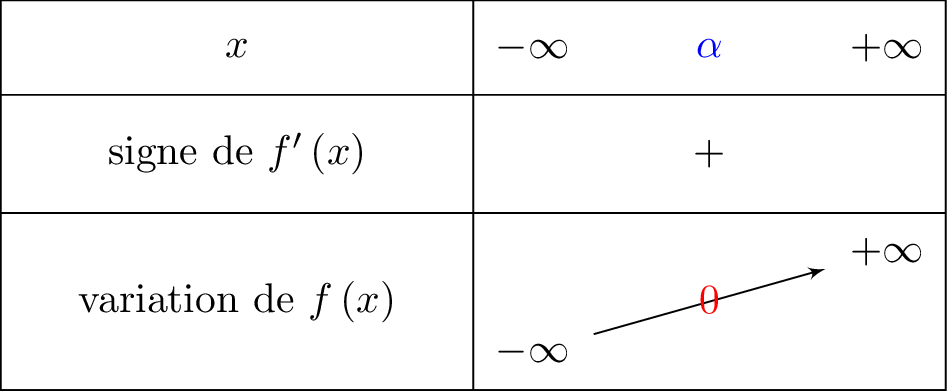
Question 6
Démontrer que appartient à l’intervalle .
Correction
A la calculatrice, on vérifie que :
et
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
et
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
Question 7
Étudier le signe de sur l’intervalle .
Correction
Sur , la fonction est continue et strictement croissante et
Donc pour tout et pour tout
On résume cela dans un tableau de signe :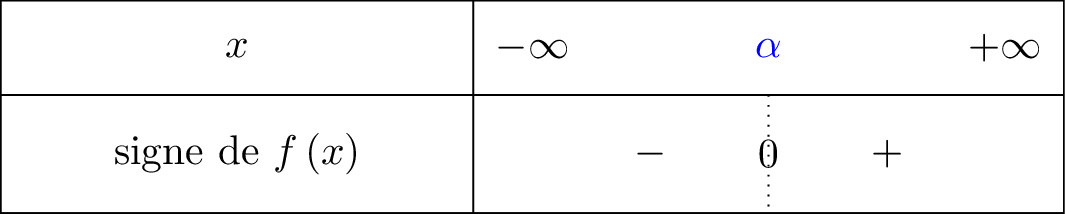 Or nous savons que ce qui nous permet de dire que sur l'intervalle , la fonction est négative.
Or nous savons que ce qui nous permet de dire que sur l'intervalle , la fonction est négative.
Donc pour tout et pour tout
On résume cela dans un tableau de signe :

Question 8
On note la fonction définie sur l’intervalle par :
Démontrer que l’équation est équivalente à l’équation .
Correction
équivaut successivement à :
. Une fois rendu, ici, il nous faut reprendre le même raisonnement que la question , que nous réécrivons ci-dessus :
: équivaut successivement à :
. Une fois rendu, ici, il nous faut reprendre le même raisonnement que la question , que nous réécrivons ci-dessus :
: équivaut successivement à :
Question 9
En déduire que est l’unique réel vérifiant : .
Correction
D'après la question , nous avons vu que était l’unique solution dans de l’équation qui est équivalente à .
Il en résulte donc que est l’unique solution dans de l’équation .
Finalement, est l’unique réel vérifiant : .
Il en résulte donc que est l’unique solution dans de l’équation .
Finalement, est l’unique réel vérifiant : .
Question 10
Calculer et montrer que
Correction
On note la fonction définie sur l’intervalle par :
est dérivable sur .
On reconnaît la forme avec et
Ainsi : et .
Il vient alors que :
. Nous avons factoriser le numérateur par
est dérivable sur .
On reconnaît la forme avec et
Ainsi : et .
Il vient alors que :
. Nous avons factoriser le numérateur par
Question 11
En déduire que la fonction est croissante sur l’intervalle .
Correction
Nous savons que
Pour tout réel , nous savons que et . De ce fait, le signe de est alors dépend du signe de .
D'après la question , sur l'intervalle , la fonction est négative. Ainsi
Il en résulte donc que, pour tout réel , et de ce fait, pour tout réel , la fonction est strictement croissante.
Pour tout réel , nous savons que et . De ce fait, le signe de est alors dépend du signe de .
D'après la question , sur l'intervalle , la fonction est négative. Ainsi
Il en résulte donc que, pour tout réel , et de ce fait, pour tout réel , la fonction est strictement croissante.
Question 12
On considère la suite définie par : et, pour tout entier naturel , par :
Démontrer par récurrence que, pour tout entier naturel :
Correction
Pour tout entier naturel , posons la propriété
Etape d'initialisation
On sait que et
ainsi .
La propriété est vraie.
Etape d'hérédité
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire et vérifions si la propriété est également vraie au rang c'est-à-dire
Par hypothèse de récurrence :
, or la fonction est croissante sur l'intervalle ainsi l'ordre sera conservé.
.
Nous savons que et que d'après la question .
De plus et que .
Cela nous donne :
Ainsi la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire pour tout entier naturel :
Etape d'initialisation
On sait que et
ainsi .
La propriété est vraie.
Etape d'hérédité
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire et vérifions si la propriété est également vraie au rang c'est-à-dire
Par hypothèse de récurrence :
, or la fonction est croissante sur l'intervalle ainsi l'ordre sera conservé.
.
Nous savons que et que d'après la question .
De plus et que .
Cela nous donne :
Ainsi la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire pour tout entier naturel :
Question 13
En déduire que la suite est convergente. On note sa limite.
Correction
Nous venons de montrer que . Cela signifie donc que . Autrement dit la suite est croissante.
De plus, comme alors qui nous permet de conclure que la suite est majorée par .
D'après le théorème de convergence des suites monotones , on peut affirmer que la suite est convergente et admet donc une limite que l'on note .
De plus, comme alors qui nous permet de conclure que la suite est majorée par .
- Une suite décroissante et minorée est convergente, elle admet donc une limite finie.
- Une suite croissante et majorée est convergente, elle admet donc une limite finie.
Question 14
Justifier l’égalité : . En déduire la valeur de .
Correction
Comme la suite est convergente alors elle admet une limite que l'on note .
Nous pouvons écrire que :
Or la fonction est continue donc .
Comme alors
Nous avons alors et
Ainsi :
D'après la question , nous savons que est l’unique réel vérifiant : .
Par conséquent :
Nous pouvons écrire que :
Or la fonction est continue donc .
Comme alors
Nous avons alors et
Ainsi :
D'après la question , nous savons que est l’unique réel vérifiant : .
Par conséquent :