Les probabilités conditionnelles et loi binomiale
Exercices types : Des probas et des suites (celui que vous aurez à votre DS) c'est sur :) - Exercice 1
40 min
60
Une plateforme informatique propose deux types de jeux vidéo : un jeu de type et un jeu de type .
Question 1
On admet que, dès que le joueur achève une partie, la plateforme lui propose une nouvelle partie selon le modèle suivant :
si le joueur achève une partie de type , la plateforme lui propose de jouer à nouveau une partie de type avec une probabilité de ; si le joueur achève une partie de type , la plateforme lui propose de jouer à nouveau une partie de type avec une probabilité de . Pour un entier naturel supérieur ou égal à , on note et les évènements :
: « la n-ième partie est une partie de type . »
: « la n-ième partie est une partie de type . »
Pour tout entier naturel supérieur ou égal à , on note la probabilité de l’évènement .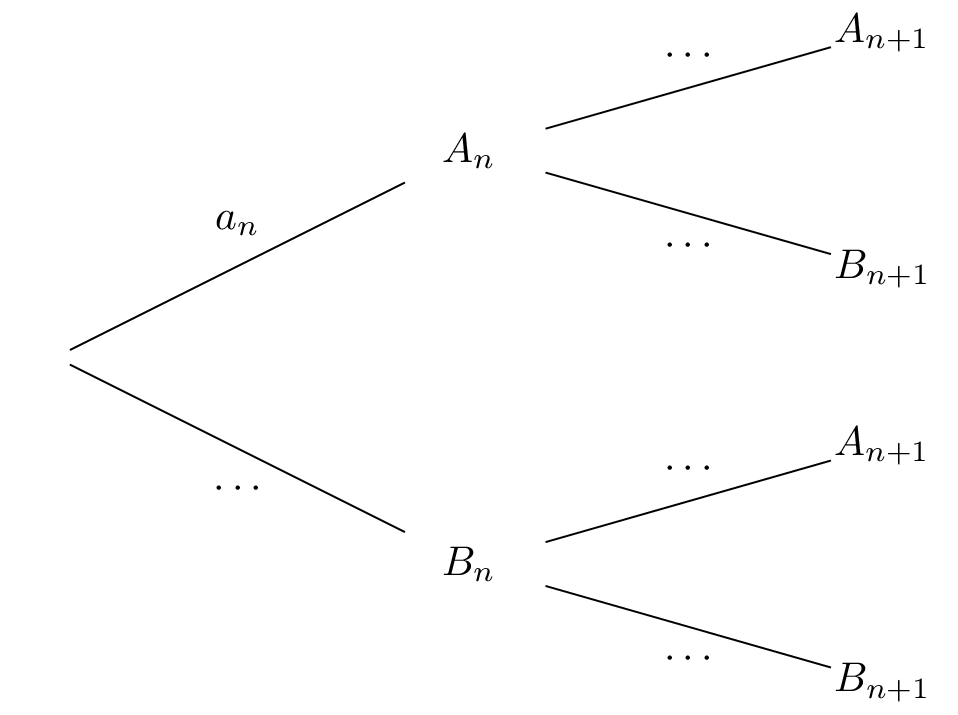
: « la n-ième partie est une partie de type . »
: « la n-ième partie est une partie de type . »
Pour tout entier naturel supérieur ou égal à , on note la probabilité de l’évènement .

Recopier et compléter l’arbre pondéré ci-dessus.
Correction
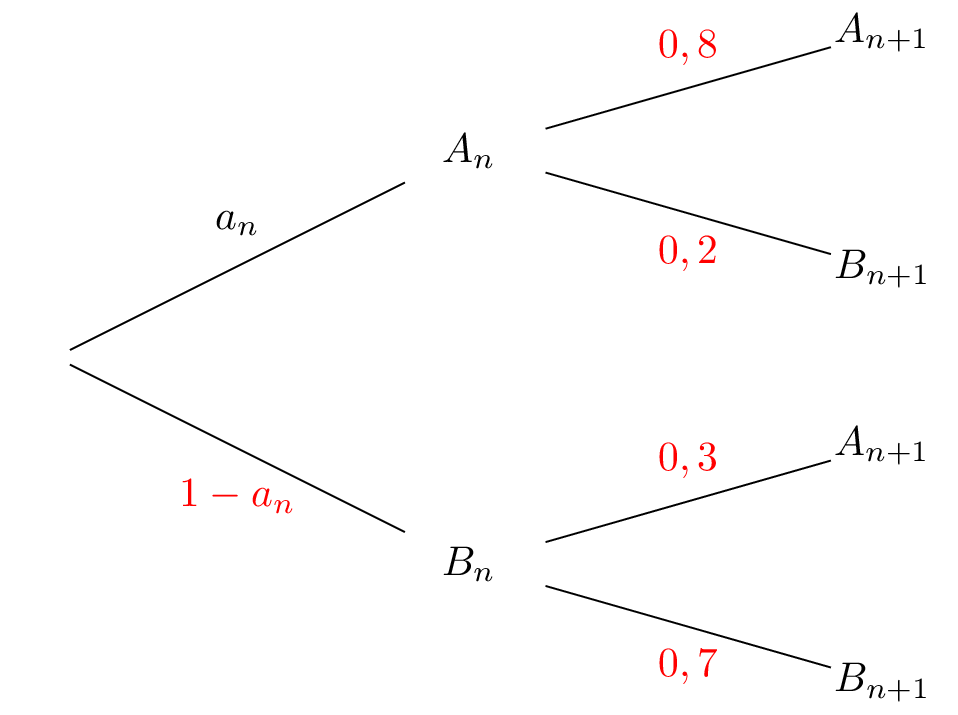
Question 2
Montrer que pour tout entier naturel , on a :
Correction

Il vient alors que la probabilité de l'évènement . Autrement dit :
Les évènements et forment une partition de l'univers.
D'après la loi des probabilités totales, on a :
Ainsi :
Question 3
Dans la suite de l’exercice, on note la probabilité que le joueur joue au jeu lors de sa première partie, où est un nombre réel appartenant à l’intervalle . La suite est donc définie par : , et pour tout entier naturel , on a : .
Pour les questions , et , on suppose que .
Pour les questions , et , on suppose que .
Montrer par récurrence, que pour tout entier naturel , on a :
Correction
Pour tout entier naturel , posons la propriété
Etape d'initialisation
On sait que ainsi .
La propriété est vraie.
Etape d'hérédité
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire et vérifions si la propriété est également vraie au rang c'est-à-dire
Par hypothèse de récurrence :
, on multiplie par de part et d'autre de l'inégalité
, on ajoute de part et d'autre de l'inégalité. Il vient alors que :
Ainsi :
et on peut alors écrire que :
d'où :
Ainsi la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel , on a bien :
Etape d'initialisation
On sait que ainsi .
La propriété est vraie.
Etape d'hérédité
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire et vérifions si la propriété est également vraie au rang c'est-à-dire
Par hypothèse de récurrence :
, on multiplie par de part et d'autre de l'inégalité
, on ajoute de part et d'autre de l'inégalité. Il vient alors que :
Ainsi :
et on peut alors écrire que :
d'où :
Ainsi la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel , on a bien :
Question 4
Montrer que la suite est croissante .
Correction
Nous savons que :
Pour étudier les variations de la suite , il nous faut étudier le signe .
Ainsi :
. Nous allons étudier le signe de
D'après la question précédente, nous avons vu que : . D'où :
. Nous avons changé le sens de l'inéquation car on nous avons multiplié par un nombre négatif. Que l'on peut aussi écrire :
. Nous rajoutons de part et d'autre de l'inégalité :
. Or :
Il vient alors que :
Il en résulte donc que .
La suite est bien croissante .
Pour étudier les variations de la suite , il nous faut étudier le signe .
Ainsi :
. Nous allons étudier le signe de
D'après la question précédente, nous avons vu que : . D'où :
. Nous avons changé le sens de l'inéquation car on nous avons multiplié par un nombre négatif. Que l'on peut aussi écrire :
. Nous rajoutons de part et d'autre de l'inégalité :
. Or :
Il vient alors que :
Il en résulte donc que .
La suite est bien croissante .
Question 5
Montrer que la suite est convergente.
Correction
- Une suite décroissante et minorée est convergente, elle admet donc une limite finie.
- Une suite croissante et majorée est convergente, elle admet donc une limite finie.
D'après la question , la suite est croissante.
D'après le théorème de convergence des suites monotones , on peut affirmer que la suite est convergente et admet donc une limite que l'on note .
Question 6
Pour les questions de à , le réel appartient à l’intervalle .
On considère la suite définie pour tout entier naturel par .
On considère la suite définie pour tout entier naturel par .
Montrer que la suite est une suite géométrique.
Correction
Pour tout entier naturel
Nous savons que et que .
Ainsi :
On va écrire maintenant l'expression au rang , il vient alors que :
. On remplace l'expression de par .
Or donc
Ainsi la suite est géométrique de raison et de premier terme donc
Nous savons que et que .
Ainsi :
On va écrire maintenant l'expression au rang , il vient alors que :
. On remplace l'expression de par .
Or donc
Ainsi la suite est géométrique de raison et de premier terme donc
Question 7
En déduire que pour tout entier naturel , on a : .
Correction
- Soit une suite géométrique .
- L'expression de en fonction de est donnée par la formule
On sait que : donc
Il vient alors que :
Question 8
Déterminer la limite de la suite . Cette limite dépend-elle de la valeur de ?
Correction
D'après la question précédente, nous savons que : Comme alors :
Ainsi :
Cette limite ne dépend pas de la valeur de car le résultat de la limite ne s'exprime pas avec .
- Si alors .
- Si alors .
Ainsi :
Cette limite ne dépend pas de la valeur de car le résultat de la limite ne s'exprime pas avec .
Question 9
La plateforme diffuse une publicité insérée en début des parties de type et une autre insérée en début des parties de type . Quelle devrait-être la publicité la plus vue par un joueur s’adonnant intensivement aux jeux vidéo?
Correction
Sur le long terme, la probabilité que le joueur fasse une partie de type est et donc celle qu’il fasse une partie de type est . Le joueur verra plus souvent la publicité insérée dans les jeux de type .