Les probabilités conditionnelles et loi binomiale

Exercice 3 - Exercice 1

1 min
0
Amélie est en vacances dans une très grande métropole.
Elle doit traverser cette ville en suivant l'avenue principale, qui est jalonnée de nombreux feux tricolores.
Pour tout entier naturel n≥1n\ge 1 , on note EnE_{n} l'évènement « Amélie est arrêtée par le nen^{e} feu rouge ou orange » et En‾\overline{E_{n} }, l'évènement contraire.
Le feu orange est considéré comme un feu rouge.
Soit pnp_{n} la probabilité de EnE_{n} et (1−pn)\left(1-p_{n} \right) celle de En‾\overline{E_{n} }.
La probabilité que le premier feu tricolore soit rouge ou orange vaut 18\frac{1}{8} .
On suppose que les deux conditions suivantes sont réalisées :
  • la probabilité que le (n+1)e(n+1)^{e} feu tricolore soit rouge ou orange, si le niemen^{ieme} feu est rouge ou orange, vaut 120\frac{1}{20}
  • la probabilité que le (n+1)e(n+1)^{e} feu tricolore soit rouge ou orange, si le niemen^{ieme} feu est vert, est égale à 920\frac{9}{20}

On s'intéresse, tout d'abord, aux deux premiers feux tricolores.
Question 1

Recopier et compléter l'arbre pondéré ci-dessous.

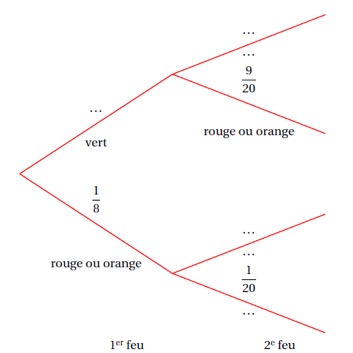
Correction
D'après l'énoncé, on a :
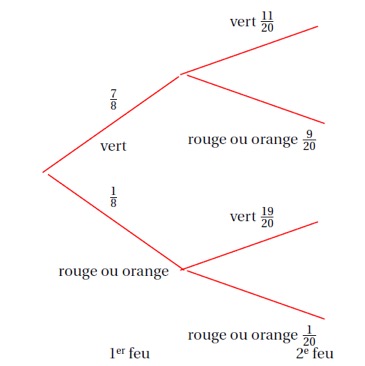
Question 2
On note XX la variable aléatoire égale au nombre de feux verts parmi ces deux feux tricolores.

Déterminer la loi de probabilité de XX.

Correction
On peut avoir, 00, 11 ou 22 feux verts.
Ainsi, d'après l'arbre, on a :
  • p(X=0)=18×120=1160p\left(X=0\right)=\frac{1}{8} \times \frac{1}{20} =\frac{1}{160} ;
  • p(X=1)=18×1920+78×920=19+63160=82160p\left(X=1\right)=\frac{1}{8} \times \frac{19}{20} +\frac{7}{8} \times \frac{9}{20} =\frac{19+63}{160} =\frac{82}{160} ;
  • p(X=2)=78×1120=77160p\left(X=2\right)=\frac{7}{8} \times \frac{11}{20} =\frac{77}{160}

On a bien p(X=0)+p(X=1)+p(X=2)=1+82+77160=1p\left(X=0\right)+p\left(X=1\right)+p\left(X=2\right)=\frac{1+82+77}{160} =1
On traduit cela dans un tableau.
Il vient alors que :
Question 3

Calculer l'espérance mathématique de XX.

Correction

On appelle l’espérance mathématique de la variable XX, la quantité notée E(X)E\left(X\right) définie par :
E(X)=∑xi×pi=x1×p1+x2×p2+…+xn×pnE\left(X\right)=\sum x_{i} \times p_{i} =x_{1} \times p_{1}+x_{2} \times p_{2}+\ldots+ x_{n} \times p_{n}

D'après la question précédente, nous savons que :

Il vient que :
E(X)=0×1160+1×82160+2×77160E\left(X\right)=0\times \frac{1}{160} +1\times \frac{82}{160} +2\times \frac{77}{160} équivaut successivement à
E(X)=82+154160E\left(X\right)=\frac{82+154}{160}
E(X)=236160E\left(X\right)=\frac{236}{160}
E(X)=5940E\left(X\right)=\frac{59}{40}
E(X)≈1,5E\left(X\right)\approx 1,5
Sur 2 feux rencontrés on aura à peu près 1,5 feux verts.
Question 4
On se place maintenant dans le cas général.

Donner les probabilités conditionnelles pEn(En+1)p_{E_{n} } \left(E_{n} +1\right) et pEn‾(En+1)p_{\overline{E_{n} }} \left(E_{n+1} \right).

Correction
D'après l'énoncé pEn(En+1)=120p_{E_{n} } \left(E_{n+1} \right)=\frac{1}{20} et pEn‾(En+1)=920p_{\overline{E_{n} }} \left(E_{n+1} \right)=\frac{9}{20} .
Question 5

En remarquant que En+1=(En+1∩En)∪(En+1∩En‾)E_{n+1} =\left(E_{n+1} \cap E_{n} \right)\cup \left(E_{n+1} \cap \overline{E_{n} }\right), montrer que, pour tout n >> 1, pn+1=920−820pnp_{n+1} =\frac{9}{20} -\frac{8}{20} p_{n}

Correction
On sait que p(En+1)=pn+1p\left(E_{n+1} \right)=p_{n+1}
D'après la loi des probabilités totales :
p(En+1)=p(En+1∩En)+p(En+1∩En‾)p\left(E_{n+1} \right)=p\left(E_{n+1} \cap E_{n} \right)+p\left(E_{n+1} \cap \overline{E_{n} }\right)
p(En+1)=p(En)×pEn(En+1)+p(En‾)×pEn‾(En+1)p\left(E_{n+1} \right)=p(E_{n} )\times p_{E_{n} } \left(E_{n+1} \right)+p(\overline{E_{n} })\times p_{\overline{E_{n} }} \left(E_{n+1} \right)
p(En+1)=pn×120+(1−pn)×920p\left(E_{n+1} \right)=p_{n} \times \frac{1}{20} +\left(1-p_{n} \right)\times \frac{9}{20}
p(En+1)=120pn+920−920pnp\left(E_{n+1} \right)=\frac{1}{20} p_{n} +\frac{9}{20} -\frac{9}{20} p_{n}
p(En+1)=920−820pnp\left(E_{n+1} \right)=\frac{9}{20} -\frac{8}{20} p_{n}
Ainsi : pn+1=920−820pnp_{n+1} =\frac{9}{20} -\frac{8}{20} p_{n}
Question 6
Soit la suite (un)(u_{n} ) de nombres réels définie pour tout entier naturel n≥1n\ge 1 par un=28pn−9u_{n} =28p_{n} -9

Montrer que (un)(u_{n} ) est une suite géométrique et déterminer sa raison.

Correction
On a :
un=28pn−9u_{n} =28p_{n} -9
un+1=28pn+1−9u_{n+1} =28p_{n+1} -9
un+1=28(920−820pn)−9u_{n+1} =28\left(\frac{9}{20} -\frac{8}{20} p_{n} \right)-9
un+1=28×920−28×820pn−9u_{n+1} =28\times \frac{9}{20} -28\times \frac{8}{20} p_{n} -9
un+1=635−565pn−9u_{n+1} =\frac{63}{5} -\frac{56}{5} p_{n} -9
un+1=185−565pnu_{n+1} =\frac{18}{5} -\frac{56}{5} p_{n}
Or, un=28pn−9u_{n} =28p_{n} -9 donc un+928=pn\frac{u_{n} +9}{28} =p_{n}
un+1=185−565×(un+928)u_{n+1} =\frac{18}{5} -\frac{56}{5} \times \left(\frac{u_{n} +9}{28} \right)
un+1=185−565×un28−565×928u_{n+1} =\frac{18}{5} -\frac{56}{5} \times \frac{u_{n} }{28} -\frac{56}{5} \times \frac{9}{28}
un+1=185−25×un−185u_{n+1} =\frac{18}{5} -\frac{2}{5} \times u_{n} -\frac{18}{5}
un+1=−25×unu_{n+1} =-\frac{2}{5} \times u_{n}
La suite (un)\left(u_{n} \right) est une suite géométrique de raison −25-\frac{2}{5} , de premier terme u1=28p1−9=28×18−9=−112u_{1} =28p_{1} -9=28\times \frac{1}{8} -9=-\frac{11}{2} .
Question 7

Exprimer unu_{n} , puis pnp_{n} en fonction de nn.

Correction
D'une part, l'expression de unu_{n} en fonction de nn.
On sait qu'alors pour n≥1n\ge 1, un=−112×(−25)n−1u_{n} =-\frac{11}{2} \times \left(-\frac{2}{5} \right)^{n-1} .

D'autre part , l'expression de pnp_{n} en fonction de nn.
Or,
un=28pn−9u_{n} =28p_{n} -9 donc
pn=un+928p_{n} =\frac{u_{n} +9}{28}
pn=un28+928p_{n} =\frac{u_{n} }{28} +\frac{9}{28}
pn=128[−112×(−25)n−1]+928p_{n} =\frac{1}{28} \left[-\frac{11}{2} \times \left(-\frac{2}{5} \right)^{n-1} \right]+\frac{9}{28}
Question 8

Déterminer la limite, si elle existe, de pnp_{n} , quand nn tend vers +∞+\infty .
Donner une interprétation de ce résultat.

Correction
Comme −1<−25<1-1<-\frac{2}{5} <1, on sait que lim⁡n→+∞(−25)n−1=0\lim\limits_{n\to +\infty } \left(-\frac{2}{5} \right)^{n-1} =0 et lim⁡n→+∞−112×(−25)n−1=0\lim\limits_{n\to +\infty } -\frac{11}{2} \times \left(-\frac{2}{5} \right)^{n-1} =0 donc par limite de somme : lim⁡n→+∞pn=928≈0,32\lim\limits_{n\to +\infty } p_{n} =\frac{9}{28} \approx 0,32.
Sur un grand nombre de feux rencontrés la probabilité qu'Amélie rencontre un feu orange ou rouge est donc à peu près de 11 sur 33.