QCM : Expert - Exercice 1

$${\color{red}\text{L'affirmation est vraie.}}$$
Nous allons commencer par résoudre dans $$\mathbb{C}$$ l'équation $$z\left(z^{2} -8z+32\right)=0$$. Il s'agit d'une équation produit nul .
$$z=0$$ ou $$z^{2} -8z+32=0$$
$$\red{\text{ D'une part :}}$$ $$z=0$$ est la première racine (solution)
$$\red{\text{ D'autre part :}}$$ $$z^{2} -8z+32=0$$
$$\Delta =-64$$, il existe donc deux racines complexes conjuguées notées $$z_{1}$$et $$z_{2}$$ tels que $$z_{1} =\frac{-b-i\sqrt{-\Delta } }{2a}$$ et $$z_{2} =\frac{-b+i\sqrt{-\Delta } }{2a}$$
et
Les racines (solutions) de l'équation $$z\left(z^{2} -8z+32\right)=0$$ sont alors $$S=\left\{0;4-4i;4+4i \right\}$$
Soient les points $$A$$ et $$B$$ d'affixes $$z_{1}$$ et $$z_{2}$$ . L'origine du repère est le point $$O$$ d'affixe $$z=0$$.
On vérifie facilement que $$\left|z_{A} \right|=\left|z_{B} \right|$$ . Autrement dit le triangle $$AOB$$ est isocèle en $$O$$.
Soit $$C$$ le milieu de $$\left[BA\right]$$ d'où :
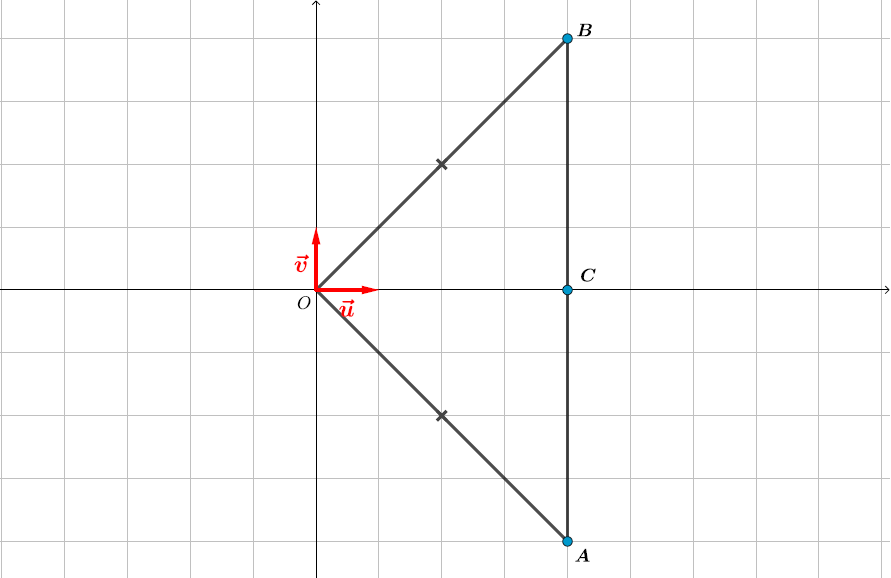
$$z_{C} =\frac{z_{1} +z_{2} }{2} =4$$ et ainsi : $$\left|z_{C} \right|=OC=4$$
Le triangle $$AOB$$ admet donc comme aire :
$$\text{Aire}\left(AOB\right)=\frac{\text{base}\times \text{hauteur}}{2}$$
$$\text{Aire}\left(AOB\right)=\frac{OC\times AB}{2}$$
Or :
$$AB=\left|z_{B} -z_{A} \right|=\left|4+4i-\left(4-4i\right)\right|=\left|8i\right|=8$$
Finalement :

$${\color{red}\text{L'affirmation est fausse.}}$$
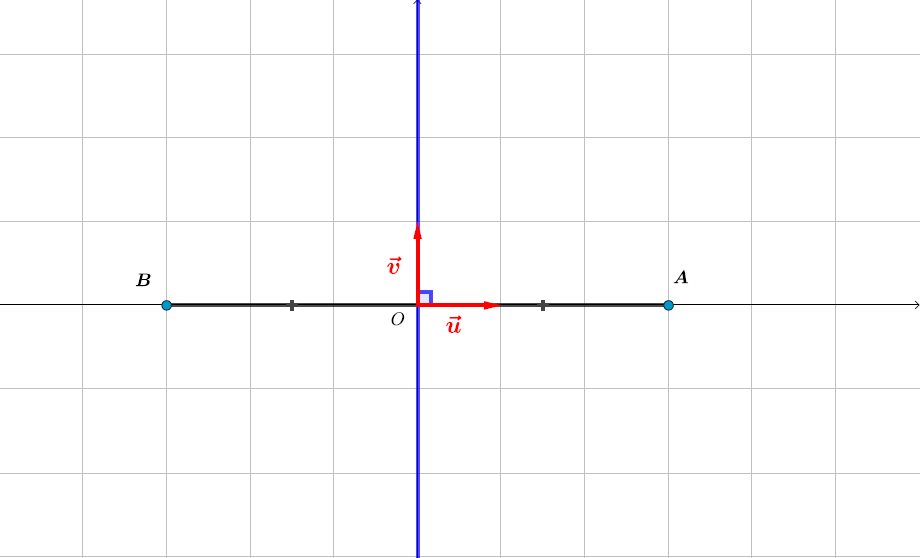
Soit $$z$$ le point d'affixe $$M$$.
On pose $$z_{A} =3$$ et $$z_{B} =-3$$ ainsi $$\left|z-z_{A} \right|=\left|z-z_{B} \right|$$
Il en résulte que $$AM=BM$$
L'ensemble des points $$M$$ du plan tel que $$\left|z-3\right|=\left|z+3\right|$$ est la médiatrice du segment $$\left[AB\right]$$ .

$${\color{red}\text{L'affirmation est vraie.}}$$Soient $$M_{n}$$ le point d’affixe $$z_{n}$$ ; $$M_{n+3}$$ le point d’affixe $$z_{n+3}$$ et $$O$$ le point d'affixe $$z_{O}=0$$
$$\left(\overrightarrow{OM_{n}} ;\overrightarrow{OM_{n+3}} \right)=\arg \left(\frac{z_{n+3} -z_{0} }{z_{n} -z_{0} } \right)$$ équivaut successivement à :
$$\left(\overrightarrow{OM_{n}} ;\overrightarrow{OM_{n+3}} \right)=\arg \left(\frac{z_{n+3} }{z_{n} } \right)$$
$$\left(\overrightarrow{OM_{n}} ;\overrightarrow{OM_{n+3}} \right)=\arg \left(\frac{\left(1-i\sqrt{3} \right)^{n+3} }{\left(1-i\sqrt{3} \right)^{n} } \right)$$
$$\left(\overrightarrow{OM_{n}} ;\overrightarrow{OM_{n+3}} \right)=\arg \left(\left(1-i\sqrt{3} \right)^{n+3-n} \right)$$
$$\left(\overrightarrow{OM_{n}} ;\overrightarrow{OM_{n+3}} \right)=\arg \left(\left(1-i\sqrt{3} \right)^{3} \right)$$
Maintenant, calculons la valeur algébrique de $$\left(1-i\sqrt{3} \right)^{3}$$ .
$$\left(1-i\sqrt{3} \right)^{3} =\left(1-i\sqrt{3} \right)^{2} \times \left(1-i\sqrt{3} \right)$$
$$\left(1-i\sqrt{3} \right)^{3} =\left(1-2i\sqrt{3} -3\right)\times \left(1-i\sqrt{3} \right)$$
$$\left(1-i\sqrt{3} \right)^{3} =1-i\sqrt{3} -2i\sqrt{3} -2i\sqrt{3} \times \left(-i\sqrt{3} \right)-3+3i\sqrt{3}$$
$$\left(1-i\sqrt{3} \right)^{3} =1-i\sqrt{3} -2i\sqrt{3} +2i^{2} \left(\sqrt{3} \right)^{2} -3+3i\sqrt{3}$$
$$\left(1-i\sqrt{3} \right)^{3} =1-i\sqrt{3} -2i\sqrt{3} -6-3+3i\sqrt{3}$$
$$\left(1-i\sqrt{3} \right)^{3} =-8$$
Ainsi :
$$\left(\overrightarrow{OM_{n}} ;\overrightarrow{OM_{n+3}} \right)=\arg \left(\left(1-i\sqrt{3} \right)^{3} \right)=-8$$
Or :
$$\left|-8 \right|=8$$
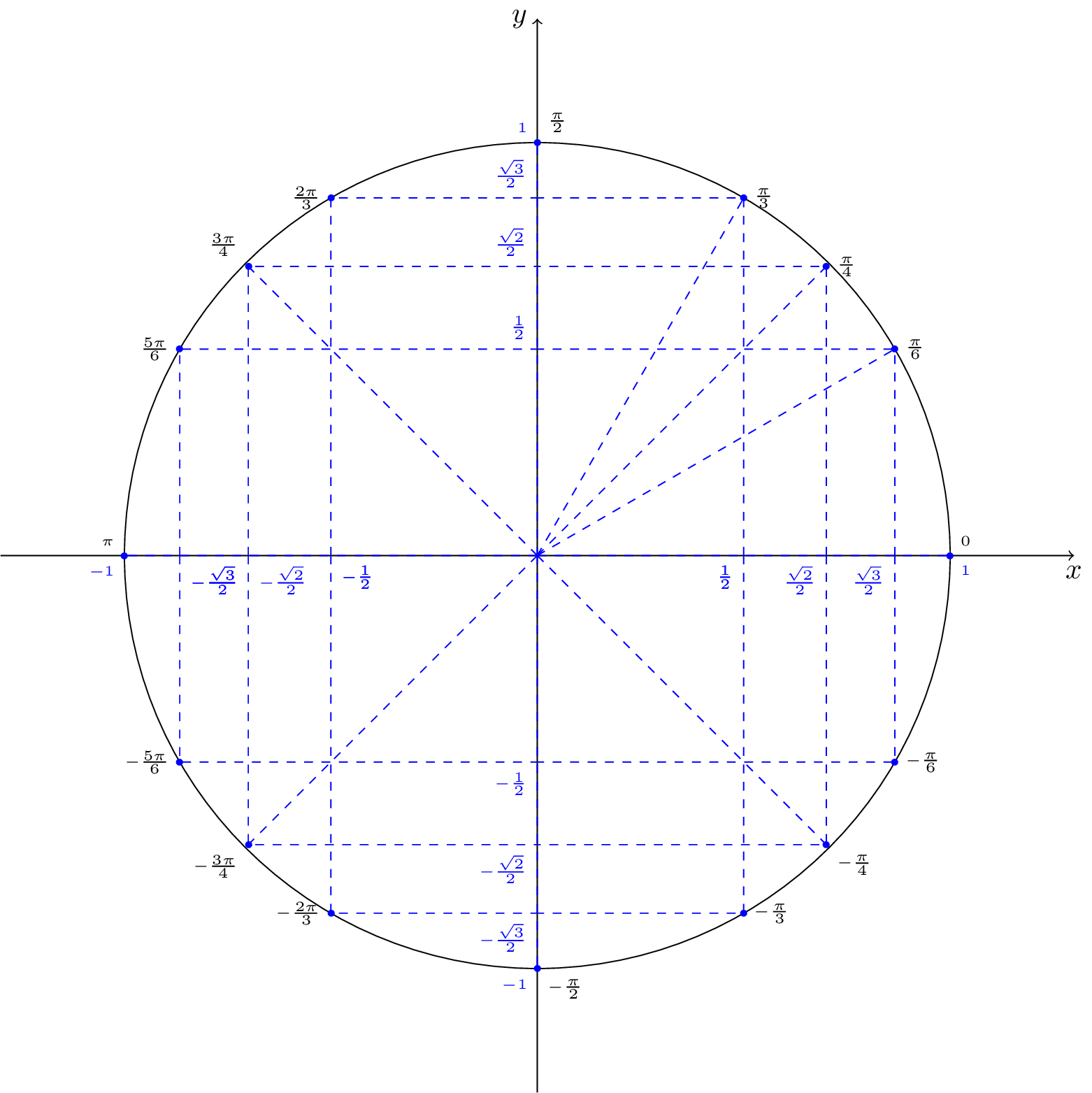
Pour l'argument $$\theta$$ on sait que $$\left\{\begin{array}{ccc} {\cos \left(\theta \right)} & {=} & {\frac{\text{partie réelle } }{\text{module } } } \\ {\sin \left(\theta \right)} & {=} & {\frac{\text{partie imaginaire } }{\text{module } } } \end{array}\right.$$
On a donc $$\left\{\begin{array}{ccc} {\cos \left(\theta \right)} & {=} & {\frac{-8}{8} } \\ {\sin \left(\theta \right)} & {=} & {\frac{0}{8} } \end{array}\right.$$
d'où $$\left\{\begin{array}{ccc} {\cos \left(\theta \right)} & {=} & {-1} \\ {\sin \left(\theta \right)} & {=} & {0} \end{array}\right.$$
Avec le cercle trigonométrique on en déduit que Finalement :
$$\left(\overrightarrow{OM_{n}} ;\overrightarrow{OM_{n+3}} \right)=\arg \left(\left(1-i\sqrt{3} \right)^{3} \right)=\arg \left(-8\right)=\pi\left[2\pi \right]$$
Pour tout entier naturel $$n$$, les points $$M_{n}$$ ; $$O$$ et $$M_{n+3}$$ sont bien alignés.