Les nombres complexes
Module et argument : sous forme de petits problèmes - Exercice 1
20 min
30
Le plan est rapporté à un repère orthonormal direct
Question 1
On considère trois points distincts , et , d’affixes , et , tels que : , et .
Calculer :
Correction
équivaut successivement :
Question 2
Donner la forme trigonométrique de .
Correction
Calculons le module et un argument de .
Nous savons que :
Pour l'argument on sait que
On a donc
d'où . Avec le cercle trigonométrique on en déduit que .
Il en résulte que la forme trigonométrique de est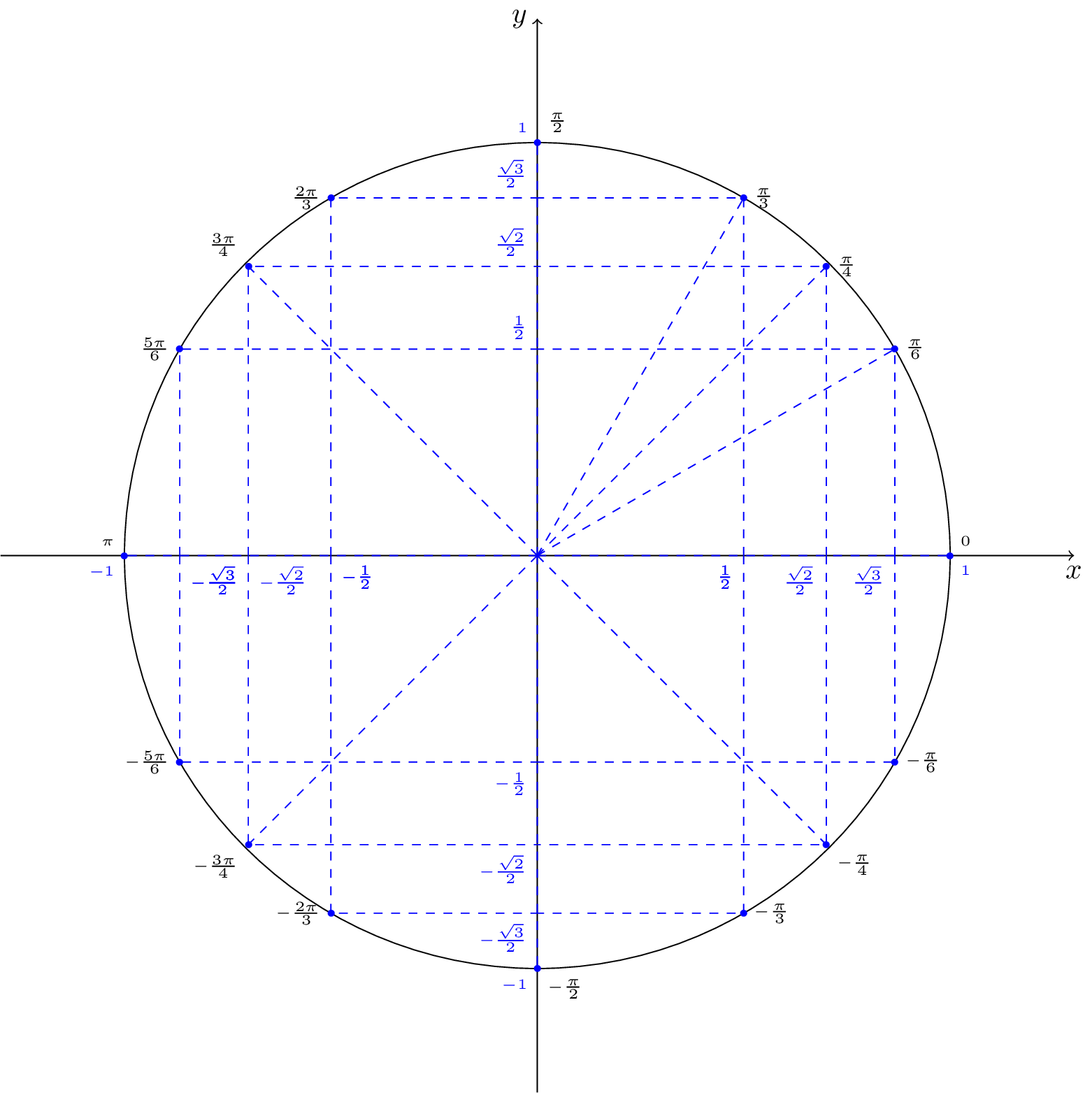
Nous savons que :
Pour l'argument on sait que
On a donc
d'où . Avec le cercle trigonométrique on en déduit que .
Il en résulte que la forme trigonométrique de est

Question 3
En déduire la nature du triangle .
Correction
et
D'une part :
équivaut successivement à :
. Or : correspond à la distance et correspond à la distance .
Ainsi :
. Il vient alors que :
.
Le triangle est isocèle en .
D'autre part :
équivaut successivement à :
Le triangle est rectangle en .
Finalement , le triangle est rectangle isocèle en .
Question 4
Soit le milieu de . Déterminer l'affixe de .
Correction
Question 5
Calculer la longueur .
Correction
Pour calculer la longueur , il faut calculer le module :
Question 6
Déterminer l’ensemble des points d’affixe tel que :
Correction
équivaut successivement à :
Le point se trouve sur le cercle de centre et de rayon .
L’ensemble des point est donc le cercle de centre et de rayon .
Le point se trouve sur le cercle de centre et de rayon .
L’ensemble des point est donc le cercle de centre et de rayon .
Question 7
Pourquoi les points , et appartiennent à l’ensemble ?
Correction
Dans un triangle rectangle le centre du cercle circonscrit se trouve au milieu de l’hypoténuse. Le point est le milieu de l’hypoténuse et le rayon du cercle est égal à la distance . L’ensemble est donc le cercle circonscrit au triangle , il passe donc par les points , et .