Exercices types : Encore des classiques - Exercice 1

Il faut chercher par tâtonnement. Il faut tester des valeurs entières le plus souvent. Avec $$0$$, cela ne marche pas. Mais avec $$1$$ oui cela fonctionne.
$$z=1$$ est une solution évidente. En effet :
$$1^{4} +2\times1^{3} -1-2=1+2-1-2=0$$

Nous allons développer l'expression $$\left(z^{2} +z-2\right)\left(z^{2} +z+1\right)$$ .
$$\left(z^{2} +z-2\right)\left(z^{2} +z+1\right)=z^{2} \times z^{2} +z^{2} \times z+z^{2} \times 1+z\times z^{2} +z\times z+z\times 1-2\times z^{2} -2\times z-2\times 1$$ équivaut successivement à :
$$\left(z^{2} +z-2\right)\left(z^{2} +z+1\right)=z^{4} +z^{3} +z^{2} +z^{3} +z^{2} +z-2z^{2} -2z-2$$

$$z^{4} +2z^{3} -z-2=0\Leftrightarrow \left(z^{2} +z-2\right)\left(z^{2} +z+1\right)=0$$
Il s'agit donc d'une équation produit nul. $$z^{2} +z-2=0$$ ou $$z^{2} +z+1=0$$

Résolution de l'équation $$z^{2} +z-2=0$$ .

$$\Delta =9$$, il existe donc deux racines réelles distinctes notées $$z_{1}$$et $$z_{2}$$ tels que $$z_{1} =\frac{-b-\sqrt{-\Delta } }{2a}$$ et $$z_{2} =\frac{-b+\sqrt{-\Delta } }{2a}$$
et

Résolution de l'équation $$z^{2} +z+1=0$$ .

$$\Delta =-3$$, il existe donc deux racines complexes conjuguées notées $$z_{3}$$ et $$z_{4}$$ tels que $$z_{3} =\frac{-b-i\sqrt{-\Delta } }{2a}$$ et $$z_{4} =\frac{-b+i\sqrt{-\Delta } }{2a}$$
et
Finalement les solutions de l'équation $$\left(E\right)$$ sont : $$S=\left\{-2;1;\frac{-1-i\sqrt{3} }{2} ;\frac{-1+i\sqrt{3} }{2} \right\}$$

Les solutions de l’équation $$\left(E\right)$$ sont les affixes de quatre points $$A$$, $$B$$, $$C$$, $$D$$ du plan complexe tels que $$ABCD$$ est un quadrilatère non croisé. Nous choisissons ainsi : $$z_{A}=-2$$ ; $$z_{B}=\frac{-1-i\sqrt{3} }{2}$$ ; $$z_{C}=1$$ et $$z_{D}=\frac{-1+i\sqrt{3} }{2}$$.
Nous représentons ce quadrilatère ci-dessous :
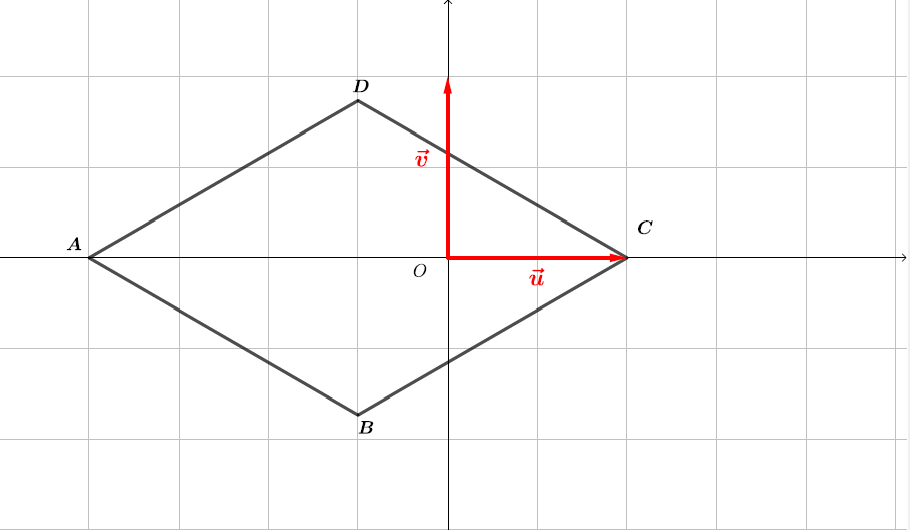On remarque que : $$\frac{z_{A} +z_{C} }{2} =-\frac{1}{2}$$ et $$\frac{z_{B} +z_{D} }{2} =-\frac{1}{2}$$. Cela signifie que les diagonales $$\left[AC\right]$$ et $$\left[BD\right]$$ ont le même milieu. De ce fait le quadrilatère $$ABCD$$ est un parallélogramme.
Vérifions maintenant si deux cotés consécutifs sont égaux.
$$AB=\left|z_{B} -z_{A} \right|\Leftrightarrow AB=\left|-\frac{1}{2} -i\frac{\sqrt{3} }{2} -\left(-2\right)\right|\Leftrightarrow AB=\left|-\frac{1}{2} -i\frac{\sqrt{3} }{2} +2\right|\Leftrightarrow AB=\left|\frac{3}{2} -i\frac{\sqrt{3} }{2} \right|$$
D'où : $$AB=\sqrt{\left(\frac{3}{2} \right)^{2} +\left(-\frac{\sqrt{3} }{2} \right)^{2} } \Leftrightarrow$$
$$AD=\left|z_{D} -z_{A} \right|\Leftrightarrow AD=\left|-\frac{1}{2} +i\frac{\sqrt{3} }{2} -\left(-2\right)\right|\Leftrightarrow AD=\left|-\frac{1}{2} +i\frac{\sqrt{3} }{2} +2\right|\Leftrightarrow AD=\left|\frac{3}{2} +i\frac{\sqrt{3} }{2} \right|$$
D'où : $$AD=\sqrt{\left(\frac{3}{2} \right)^{2} +\left(\frac{\sqrt{3} }{2} \right)^{2} } \Leftrightarrow$$
Finalement, le parallélogramme $$ABCD$$ a deux cotés consécutifs égaux. C'est bien un losange.