Les nombres complexes
Exercice 8 - Exercice 1
1 min
0
Question 1
On travaille dans le plan complexe rapporté au repère orthonormal direct . On considère les points , , et d'affixes respectives , , et .
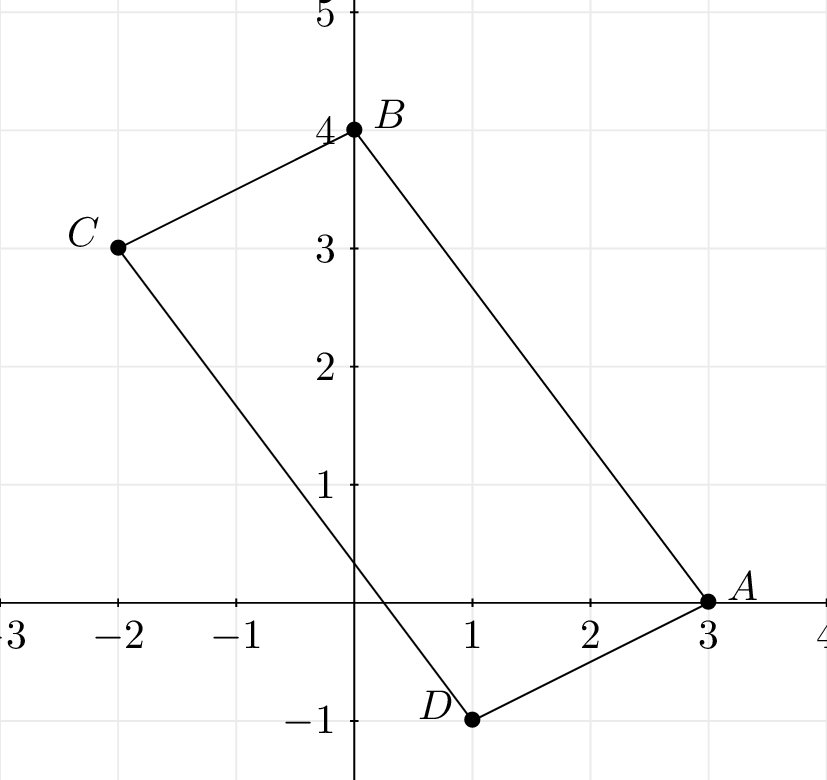
Placer les points , , et dans le plan.
Correction
Question 2
Quelle est la nature du quadrilatère ? Justifier votre réponse.
Correction
On remarque que :
.
Cela signifie que les diagonales et ont même milieu. De ce fait le quadrilatère est un parallélogramme.
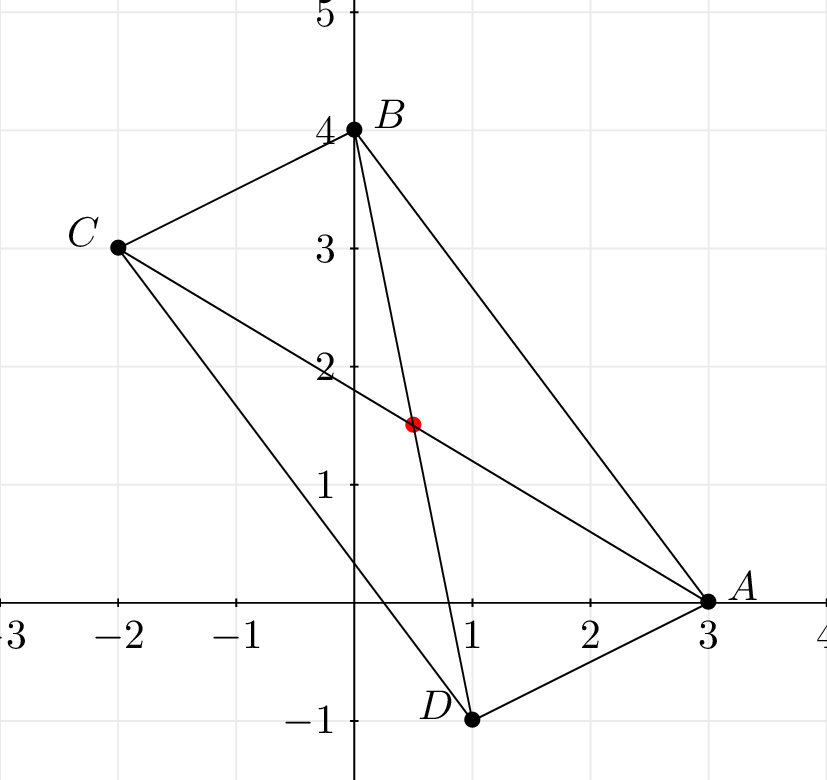
.
Cela signifie que les diagonales et ont même milieu. De ce fait le quadrilatère est un parallélogramme.

Question 3
On considère dans l’ensemble des complexes les équations : et
Montrer que est une solution de l'équation .
Correction
Il faut dans l'expression remplacer tous les par et nous devons obtenir .
Question 4
Montrer que est solution de l'équation
Correction
Il faut dans l'expression remplacer tous les par et nous devons obtenir .
Question 5
Développer puis
Correction
D'une part :
D'autre part :
D'autre part :
Question 6
En déduire les solutions de
Correction
Nous voulons résoudre
Or d'après la question précédente, nous avons vu que : et
Il en résulte donc que :
équivaut successivement à :
Il s'agit d'une équation produit nul.
Il faut donc que :
ou ou ou
Il vient alors que :
ou ou ou
Finalement :
Or d'après la question précédente, nous avons vu que : et
Il en résulte donc que :
équivaut successivement à :
Il s'agit d'une équation produit nul.
Il faut donc que :
ou ou ou
Il vient alors que :
ou ou ou
Finalement :
Question 7
Soit la solution dont la partie imaginaire est strictement négative. Donner la forme trigonométrique et exponentielle de .
Correction
Parmi les quatre solutions obtenue à la question , celle dont la partie imaginaire est strictement négative est . Ainsi .
Pour l'argument on sait que
On a donc
D'où :
Avec le cercle trigonométrique on en déduit que
Soit un nombre complexe dont le module est et un argument de .
L'écriture trigonométrique de est alors
L'écriture exponentielle de est alors
Pour l'argument on sait que
On a donc
D'où :
Avec le cercle trigonométrique on en déduit que
Soit un nombre complexe dont le module est et un argument de .
- L'écriture trigonométrique de est alors
- L'écriture exponentielle de est alors
L'écriture exponentielle de est alors
Question 8
Déterminer les entiers relatifs tels que les points d'affixes soient sur la droite d'équation .
Correction
D'où :
Les points appartenant à la droite ont un argument qui vaut et les points ont un argument qui vaut
avec
Question 9
On appelle l'application qui au point d'affixe , associe le point , d'affixe telle que :
Donner la partie réelle et la partie imaginaire de .
Correction
On pose
équivaut successivement à :
équivaut successivement à :