Les nombres complexes
Exercice 6 - Exercice 1
1 min
0
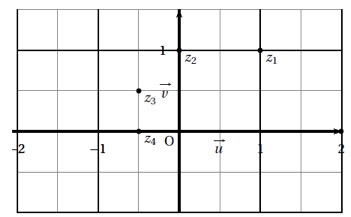
Le plan complexe est muni d'un repère orthonormal direct .
On pose et, pour tout entier naturel , .
On note le point du plan d'affixe .
On pose et, pour tout entier naturel , .
On note le point du plan d'affixe .
Question 1
Calculer , , , et vérifier que est un nombre réel.
Puis placer les points , , , et sur une figure.
Puis placer les points , , , et sur une figure.
Correction
- donc
- donc
- donc
- donc et est un nombre réel.
Question 2
Pour tout entier naturel , on pose .
Justifier que la suite est une suite géométrique puis établir que, pour tout entier naturel , .
Justifier que la suite est une suite géométrique puis établir que, pour tout entier naturel , .
Correction
On a :
équivaut successivement à
L'égalité montre que la suite est une suite géométrique de raison .
On a .
On exprime maintenant en fonction de .
Ainsi :
Finalement :
équivaut successivement à
L'égalité montre que la suite est une suite géométrique de raison .
On a .
On exprime maintenant en fonction de .
Ainsi :
Finalement :
Question 3
A partir de quel rang tous les points appartiennent-ils au disque de centre et de rayon ?
Correction
On a , donc appartient au disque (fermé) de centre O et de rayon 0,1 si et seulement si :
équivaut successivement à
La condition sera donc réalisée la première fois par .
On a donc .
La calculatrice nous donne et .
équivaut successivement à
La condition sera donc réalisée la première fois par .
On a donc .
La calculatrice nous donne et .
Question 4
Etablir que, pour tout entier naturel , .
En déduire la nature du triangle .
En déduire la nature du triangle .
Correction
Pour tout naturel , donc .
On peut donc écrire :
équivaut successivement à
Or , ainsi :
L'interprétation géométrique de cette égalité est :
Etude des modules
Comme alors :
Or est une distance et en l'occurrence la distance et est la distance .
Le triangle est isocèle en .
Etude de l'argument
Comme alors :
où
Ainsi pour tout naturel le triangle est rectangle en .
Finalement pour tout naturel , le triangle est rectangle isocèle en .
On peut donc écrire :
équivaut successivement à
Or , ainsi :
L'interprétation géométrique de cette égalité est :
Etude des modules
Comme alors :
Or est une distance et en l'occurrence la distance et est la distance .
Le triangle est isocèle en .
Etude de l'argument
Comme alors :
où
Ainsi pour tout naturel le triangle est rectangle en .
Finalement pour tout naturel , le triangle est rectangle isocèle en .
Question 5
Pour tout entier naturel , on note la longueur de la ligne brisée .
On a ainsi : .
Exprimer en fonction de .
Quelle est la limite de la suite ?
On a ainsi : .
Exprimer en fonction de .
Quelle est la limite de la suite ?
Correction
Comme les triangles sont isocèles ;
En effet, dans le triangle isocèle on a :
.
En effet,
Cette somme est la somme de premiers termes d'une suite géométrique de premier terme et de raison .
On a donc :
Calcul de la limite de la suite
On factorise le numérateur et le dénominateur par
Or et .
Par quotient après simplification, on obtient
En effet, dans le triangle isocèle on a :
.
En effet,
Cette somme est la somme de premiers termes d'une suite géométrique de premier terme et de raison .
On a donc :
Calcul de la limite de la suite
On factorise le numérateur et le dénominateur par
Or et .
Par quotient après simplification, on obtient