Les fonctions trigonométriques

Périodicité - Exercice 1

15 min
25
Question 1

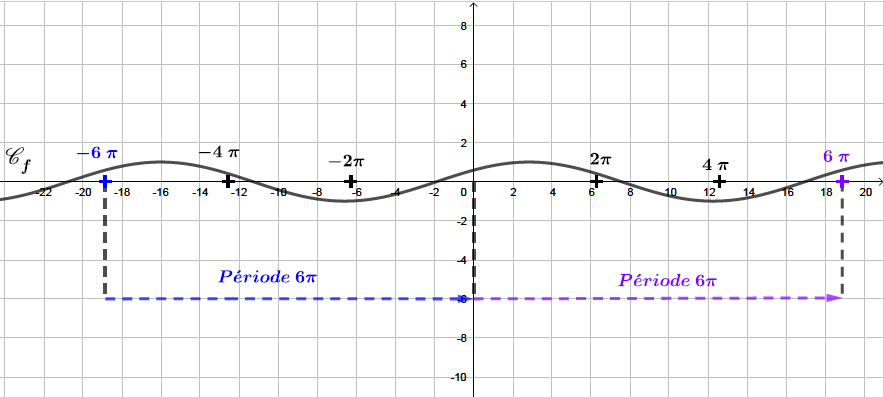
Soit f(x)=2cos⁡(x)+3sin⁡(x)f\left(x\right)=2\cos \left(x\right)+3\sin \left(x\right). Montrer que ff est 2π−2\pi -périodique.

Correction
  • ff est T−T-périodique si et seulement si f(x+T)=f(x)f\left(x+T\right)=f\left(x\right)
  • Les fonctions cosinus et sinus sont 2π−2\pi -périodique, c'est-à-dire cos⁡(x+2π)=cos⁡(x)\cos \left(x+2\pi \right)=\cos \left(x\right) et sin⁡(x+2π)=sin⁡(x)\sin \left(x+2\pi \right)=\sin \left(x\right)
    • f(x+2π)=2cos⁡(x+2π)+3sin⁡(x+2π)f\left(x+2\pi \right)=2\cos \left(x+2\pi \right)+3\sin \left(x+2\pi \right) équivaut successivement à
    f(x+2π)=2cos⁡(x)+3sin⁡(x)f\left(x+2\pi \right)=2\cos \left(x\right)+3\sin \left(x\right)
    Il en résulte que
    f(x+2π)=f(x)f\left(x+2\pi \right)=f\left(x\right)
    donc ff est 2π−2\pi -périodique.
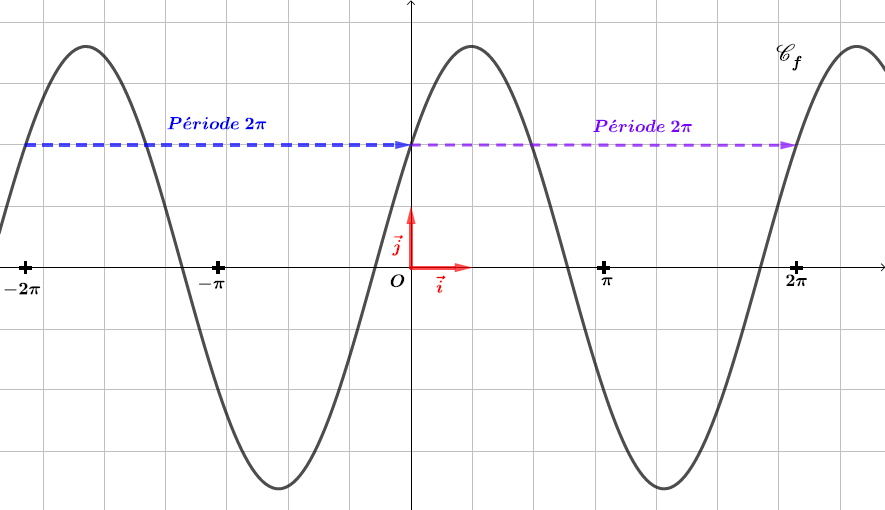
    Question 2

    Soit f(x)=−cos⁡(2x)f\left(x\right)=-\cos \left(2x\right). Montrer que ff est π−\pi -périodique.

    Correction
  • ff est T−T-périodique si et seulement si f(x+T)=f(x)f\left(x+T\right)=f\left(x\right)
  • Les fonctions cosinus et sinus sont 2π−2\pi -périodique, c'est-à-dire cos⁡(x+2π)=cos⁡(x)\cos \left(x+2\pi \right)=\cos \left(x\right) et sin⁡(x+2π)=sin⁡(x)\sin \left(x+2\pi \right)=\sin \left(x\right)
    • f(x+π)=−cos⁡(2(x+π))f\left(x+\pi \right)=-\cos \left(2\left(x+\pi \right)\right) équivaut successivement à
    f(x+π)=−cos⁡(2x+2π)f\left(x+\pi \right)=-\cos \left(2x+2\pi \right)
    f(x+π)=−cos⁡(2x)f\left(x+\pi \right)=-\cos \left(2x\right)
    Il en résulte que
    f(x+π)=f(x)f\left(x+\pi \right)=f\left(x\right)
    donc ff est π−\pi -périodique.
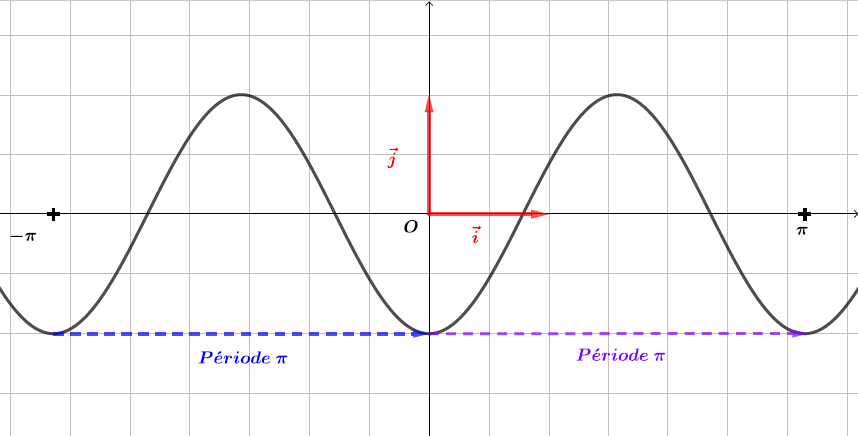
    Question 3

    Soit f(x)=sin⁡(3x+π)f\left(x\right)=\sin \left(3x+\pi \right). ff est-elle 2π3−\frac{2\pi }{3} -périodique ?

    Correction
  • ff est T−T-périodique si et seulement si f(x+T)=f(x)f\left(x+T\right)=f\left(x\right)
  • Les fonctions cosinus et sinus sont 2π−2\pi -périodique, c'est-à-dire cos⁡(x+2π)=cos⁡(x)\cos \left(x+2\pi \right)=\cos \left(x\right) et sin⁡(x+2π)=sin⁡(x)\sin \left(x+2\pi \right)=\sin \left(x\right)
    • f(x+2π3)=sin⁡(3(x+2π3)+π)f\left(x+\frac{2\pi }{3} \right)=\sin \left(3\left(x+\frac{2\pi }{3} \right)+\pi \right)
    f(x+2π3)=sin⁡(3x+2π+π)f\left(x+\frac{2\pi }{3} \right)=\sin \left(3x+2\pi +\pi \right)
    f(x+2π3)=sin⁡(3x+π)f\left(x+\frac{2\pi }{3} \right)=\sin \left(3x+\pi \right)
    f(x+2π3)=f(x)f\left(x+\frac{2\pi }{3} \right)=f\left(x\right)
    Or sin⁡(X+π)=−sin⁡(X)\sin \left(X+\pi \right)=-\sin \left(X\right)
    Donc ff est 2π3−\frac{2\pi }{3} -périodique .
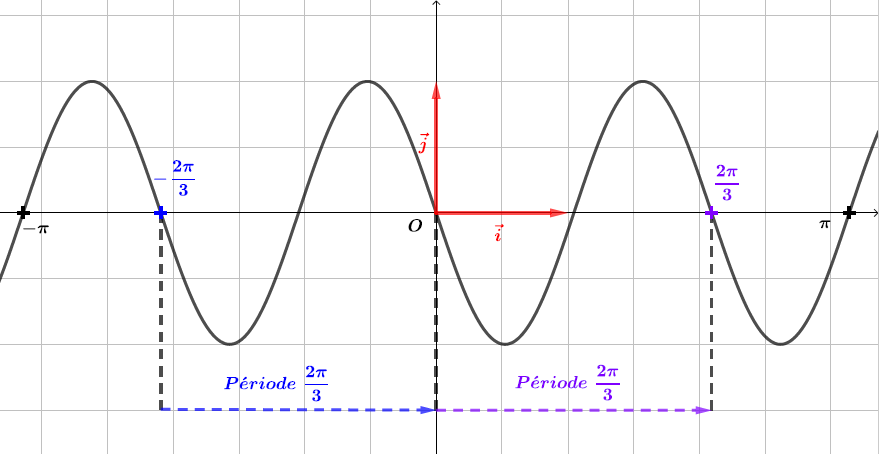
    Question 4

    f(x)=5sin⁡(x)3+cos⁡(x)f\left(x\right)=\frac{5\sin \left(x\right)}{3+\cos \left(x\right)} . ff est-elle 2π−2\pi -périodique ?

    Correction
  • ff est T−T-périodique si et seulement si f(x+T)=f(x)f\left(x+T\right)=f\left(x\right)
  • Les fonctions cosinus et sinus sont 2π−2\pi -périodique, c'est-à-dire cos⁡(x+2π)=cos⁡(x)\cos \left(x+2\pi \right)=\cos \left(x\right) et sin⁡(x+2π)=sin⁡(x)\sin \left(x+2\pi \right)=\sin \left(x\right)
    • f(x+2π)=5sin⁡(x+2π)3+cos⁡(x+2π)f\left(x+2\pi \right)=\frac{5\sin \left(x+2\pi \right)}{3+\cos \left(x+2\pi \right)}
    f(x+2π)=5sin⁡(x)3+cos⁡(x)f\left(x+2\pi \right)=\frac{5\sin \left(x\right)}{3+\cos \left(x\right)}
    f(x+2π)=f(x)f\left(x+2\pi \right)=f\left(x\right)

    Donc ff est 2π−2\pi- périodique.
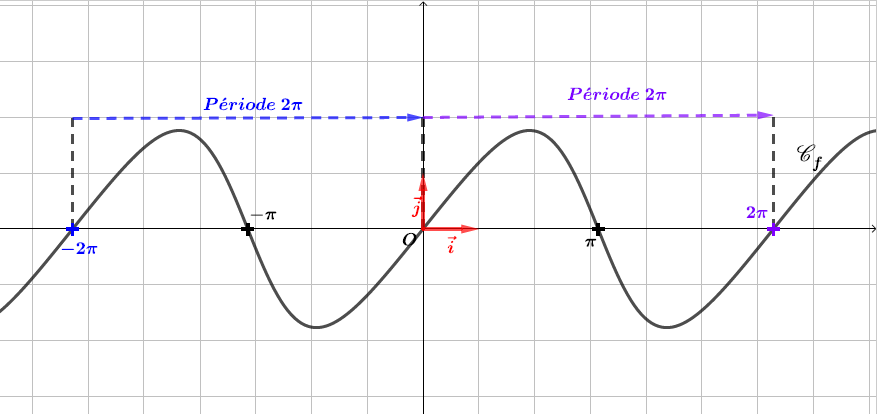
    Question 5

    f(x)=2sin⁡(x)+3sin⁡(x2)f\left(x\right)=2\sin \left(x\right)+3\sin \left(\frac{x}{2} \right) . ff est-elle 4π−4\pi -périodique ?

    Correction
  • ff est T−T-périodique si et seulement si f(x+T)=f(x)f\left(x+T\right)=f\left(x\right)
  • Les fonctions cosinus et sinus sont 2π−2\pi -périodique, c'est-à-dire cos⁡(x+2π)=cos⁡(x)\cos \left(x+2\pi \right)=\cos \left(x\right) et sin⁡(x+2π)=sin⁡(x)\sin \left(x+2\pi \right)=\sin \left(x\right) ou encore cos⁡(x+2kπ)=cos⁡(x)\cos \left(x+2k\pi \right)=\cos \left(x\right) et sin⁡(x+2kπ)=sin⁡(x)\sin \left(x+2k\pi \right)=\sin \left(x\right) où k∈Zk \in \mathbb{Z}
    • f(x+4π)=2sin⁡(x+4π)+3sin⁡(x+4π2)f\left(x+4\pi \right)=2\sin \left(x+4\pi \right)+3\sin \left(\frac{x+4\pi }{2} \right)
    f(x+4π)=2sin⁡(x+2×(2π))+3sin⁡(x2+4π2)f\left(x+4\pi \right)=2\sin \left(x+2\times \left(2\pi \right)\right)+3\sin \left(\frac{x}{2} +\frac{4\pi }{2} \right)
    f(x+4π)=2sin⁡(x+2×(2π))+3sin⁡(x2+2π)f\left(x+4\pi \right)=2\sin \left(x+2\times \left(2\pi \right)\right)+3\sin \left(\frac{x}{2} +2\pi \right)
    f(x+4π)=2sin⁡(x)+3sin⁡(x2)f\left(x+4\pi \right)=2\sin \left(x\right)+3\sin \left(\frac{x}{2} \right)
    f(x+4π)=f(x)f\left(x+4\pi \right)=f\left(x\right)

    Donc ff est 4π−4\pi- périodique.
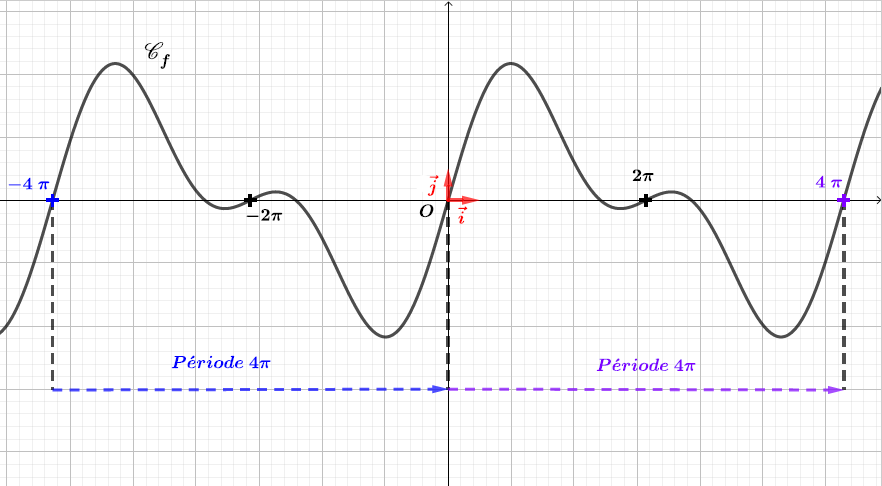
    Question 6

    f(x)=sin⁡(x3+π5)f\left(x\right)=\sin \left(\frac{x}{3} +\frac{\pi }{5} \right) . ff est-elle 6π−6\pi -périodique ?

    Correction
  • ff est T−T-périodique si et seulement si f(x+T)=f(x)f\left(x+T\right)=f\left(x\right)
  • Les fonctions cosinus et sinus sont 2π−2\pi -périodique, c'est-à-dire cos⁡(x+2π)=cos⁡(x)\cos \left(x+2\pi \right)=\cos \left(x\right) et sin⁡(x+2π)=sin⁡(x)\sin \left(x+2\pi \right)=\sin \left(x\right) ou encore cos⁡(x+2kπ)=cos⁡(x)\cos \left(x+2k\pi \right)=\cos \left(x\right) et sin⁡(x+2kπ)=sin⁡(x)\sin \left(x+2k\pi \right)=\sin \left(x\right) où k∈Zk \in \mathbb{Z}
    • f(x+6π)=sin⁡(x+6π3+π5)f\left(x+6\pi \right)=\sin \left(\frac{x+6\pi }{3} +\frac{\pi }{5} \right)
    f(x+6π)=sin⁡(x3+6π3+π5)f\left(x+6\pi \right)=\sin \left(\frac{x}{3} +\frac{6\pi }{3} +\frac{\pi }{5} \right)
    f(x+6π)=sin⁡(x3+2π+π5)f\left(x+6\pi \right)=\sin \left(\frac{x}{3} +2\pi +\frac{\pi }{5} \right)
    f(x+6π)=sin⁡(x3+π5+2π)f\left(x+6\pi \right)=\sin \left(\frac{x}{3} +\frac{\pi }{5} +2\pi \right) Or : sin⁡(x3+π5+2π)=sin⁡(x3+π5)\sin \left(\frac{x}{3} +\frac{\pi }{5} +\red{2\pi} \right)=\sin \left(\frac{x}{3} +\frac{\pi }{5} \right)
    f(x+6π)=sin⁡(x3+π5)f\left(x+6\pi \right)=\sin \left(\frac{x}{3} +\frac{\pi }{5} \right)
    f(x+6π)=f(x)f\left(x+6\pi \right)=f\left(x\right)

    Donc ff est 6π−6\pi- périodique.