La géométrie dans l'espace et produit scalaire
Exercices types : ème partie - Exercice 1
35 min
55
Question 1
L'espace est muni d'un repère orthonormé . On considère les points , , et le vecteur
Justifier que les points , et définissent un plan.
Correction
On a :
et
On vérifie aisément que les vecteurs et ne sont pas colinéaires. Donc les trois points , et ne sont pas alignés et définissent un plan.
et
On vérifie aisément que les vecteurs et ne sont pas colinéaires. Donc les trois points , et ne sont pas alignés et définissent un plan.
Question 2
Démontrer que le vecteur est orthogonal aux vecteurs et .
Correction
. Donc les vecteurs et sont orthogonaux.
. Donc les vecteurs et sont orthogonaux.
Question 3
Démontrer que le plan a pour équation cartésienne .
Correction
L'écriture cartésienne d'un plan ayant un vecteur normal s'écrit .
Ensuite pour déterminer la valeur de , on utilise les coordonnées du point .
est orthogonal à deux vecteurs et non colinéaires du plan donc est un vecteur normal à ce plan. Ensuite pour déterminer la valeur de , on utilise les coordonnées du point .
Ainsi :
. il nous reste à déterminer la valeur de . Le point appartient au plan donc les cordonnées de vérifient l'équation .
Ainsi :
Le plan a donc pour équation cartésienne :
.
Question 4
On considère la droite des points dont les coordonnées sont données par : où
Donner un vecteur directeur de la droite .
Correction
- Soit une droite définie par un point et un vecteur directeur . La droite admet donc un système d’équations paramétriques, appelé représentation paramétrique, de la forme : où
Il faut prendre les coefficients devant les afin d'avoir les coordonnées du vecteur directeur.
Question 5
La droite et le plan sont-ils sécants?
Correction
Etape 1
Commencer par vérifier si le plan et la droite ne sont pas parallèles, par conséquent le plan et la droite sont sécants.
Etape 2
Il faut résoudre le système constitué de l'écriture paramétrique de la droite et du plan pour déterminer la valeur de .
Ensuite, on substitue la valeur dans la droite pour obtenir les coordonnées du point d'intersection entre le plan et la droite.
Commencer par vérifier si le plan et la droite ne sont pas parallèles, par conséquent le plan et la droite sont sécants.
Etape 2
Il faut résoudre le système constitué de l'écriture paramétrique de la droite et du plan pour déterminer la valeur de .
Ensuite, on substitue la valeur dans la droite pour obtenir les coordonnées du point d'intersection entre le plan et la droite.
Soient : un vecteur normal du plan et un vecteur directeur de
et ne sont pas parallèles, par conséquent ils sont sécants.
où
On remplace la valeur de et dans le plan
équivaut successivement à
Ainsi :
Maintenant que nous avons la valeur de , on peut obtenir les valeurs de et
Il en résulte que
Les coordonnées du point d'intersection entre la droite et le plan est le point
Question 6
Dans cette question, on considère l’ensemble des points dont les coordonnées sont données par : où
Démontrer qu’il existe un unique point qui appartient à la fois à et à . Il n’est pas demandé de déterminer ses coordonnées.
Correction
Il existe un unique point qui appartient à la fois à et à si les coordonnées vérifient le système :
où équivaut successivement à :
Etudions la fonction définie sur .
est dérivable sur . On a donc : .
Pour tout réel , on vérifie aisément que ainsi la fonction est strictement croissante sur .
De plus :
Nous allons traduire toutes ces informations dans un tableau de variation.
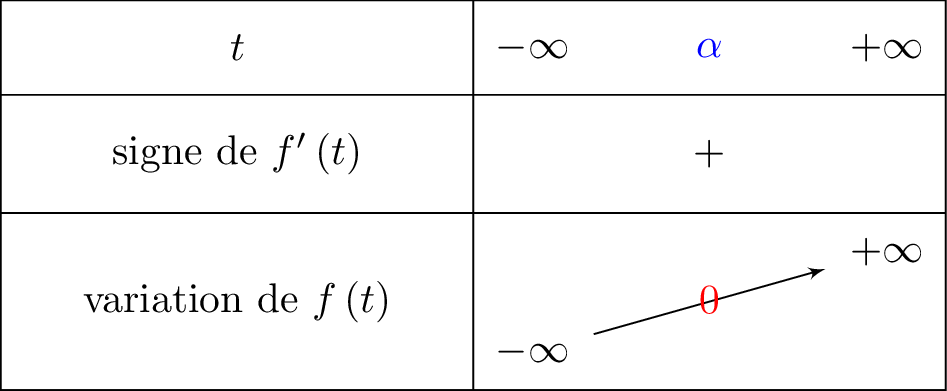
Sur , la fonction est continue et strictement croissante.
De plus, et
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que Il existe donc un unique solution de l’équation , ce qui entraîne qu’il existe un unique point d’intersection de l’ensemble et du plan .
où équivaut successivement à :
Etudions la fonction définie sur .
est dérivable sur . On a donc : .
Pour tout réel , on vérifie aisément que ainsi la fonction est strictement croissante sur .
De plus :
Nous allons traduire toutes ces informations dans un tableau de variation.
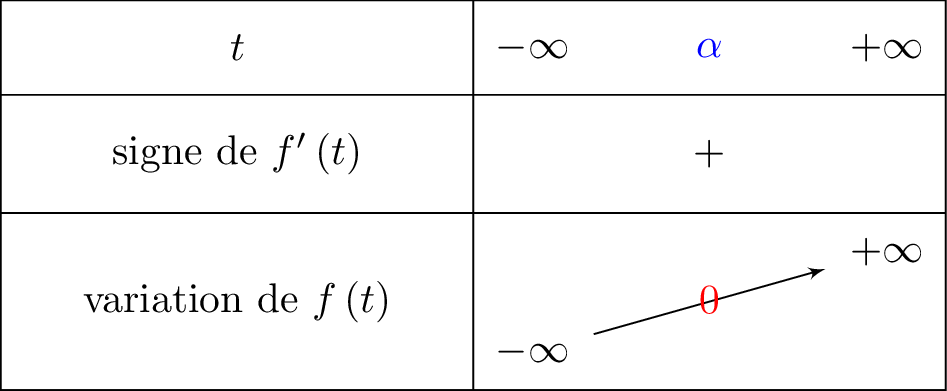
De plus, et
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que