La fonction logarithme
Primitives un peu plus compliquées - Exercice 1
15 min
25
Soit une fonction continue sur définie par
Question 1
Déterminer les réels et tels que
Correction
Nous allons mettre l'expression au même dénominateur puis résoudre un système par identification.
Il vient alors :
équivaut successivement à
On doit avoir :
Il faut que les numérateurs soient égaux.
Or deux polynômes sont égaux si et seulement si leurs coefficients respectifs sont égaux.
On en déduit le système suivant :
Il en résulte donc que :
Il vient alors :
équivaut successivement à
On doit avoir :
Il faut que les numérateurs soient égaux.
Or deux polynômes sont égaux si et seulement si leurs coefficients respectifs sont égaux.
On en déduit le système suivant :
Il en résulte donc que :
Question 2
En déduire une primitive de tel que
Correction
On sait que :
, autrement dit :
Pour calculer les primitives de .
Commençons par calculer les primitives de
On reconnait une forme
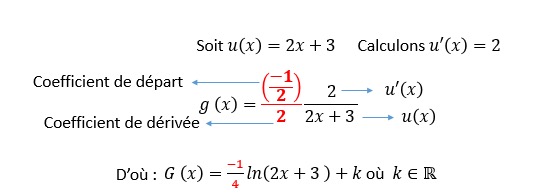
Finalement :
Or équivaut successivement à
On peut conclure que :
, autrement dit :
Pour calculer les primitives de .
Commençons par calculer les primitives de
On reconnait une forme
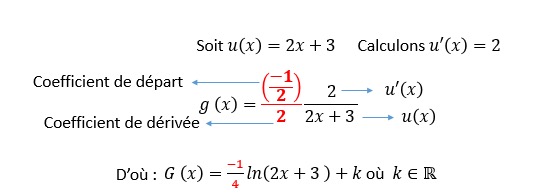
Finalement :
où
Or équivaut successivement à
On peut conclure que :