La fonction logarithme
Exercice 6 - Exercice 1
1 min
0
Pour tout réel strictement positif.
On considère la fonction définie sur par :
Soit la courbe représentative de la fonction dans le plan muni d'un repère
On considère la fonction définie sur par :
Soit la courbe représentative de la fonction dans le plan muni d'un repère
Question 1
Partie A : Mise en place d'une inégalité
On considère la fonction définie sur par : .
On considère la fonction définie sur par : .
Etudier le sens de variation de .
Correction
La fonction est dérivable sur , on a :
Comme alors et .
Il en résulte que .
La fonction est donc décroissante sur .
On traduit cela dans un tableau de variation :
 De plus, .
De plus, .
Le maximum de est donc .
Comme alors et .
Il en résulte que .
La fonction est donc décroissante sur .
On traduit cela dans un tableau de variation :

Le maximum de est donc .
Question 2
En déduire que pour tout réel positif ou nul .
Correction
Ainsi, pour tout , le maximum de est donc .
Ainsi : ou encore .
Finalement :
Ainsi : ou encore .
Finalement :
Question 3
Partie B : Etude de la fonction
définie sur par
définie sur par
Montrer que pour tout réel appartenant à l'intervalle , .
En déduire la limite de en .
En déduire la limite de en .
Correction
équivaut successivement à
Or ainsi .
On pose et
Finalement, par composition
La courbe admet une asymptote horizontale d'équation au voisinage de plus l'infini.
Or ainsi .
On pose et
Finalement, par composition
La courbe admet une asymptote horizontale d'équation au voisinage de plus l'infini.
Question 4
Calculer pour tout réel appartenant à l'intervalle et en déduire le sens de variation de la fonction .
Correction
La fonction est dérivable sur et :
équivaut successivement à
Pour tout réel , le dénominateur est strictement positif.
Le signe de est alors du signe de .
Or,
Il vient alors que :
la fonction est donc positive sur et négative sur .
Finalement, la fonction est donc croissante sur et décroissante sur .
équivaut successivement à
Pour tout réel , le dénominateur est strictement positif.
Le signe de est alors du signe de .
Or,
Il vient alors que :
la fonction est donc positive sur et négative sur .
Finalement, la fonction est donc croissante sur et décroissante sur .
Question 5
Dresser le tableau de variation de .
Correction
Suite aux informations obtenues à la question 2, on dresse le tableau de variation ci-dessous :
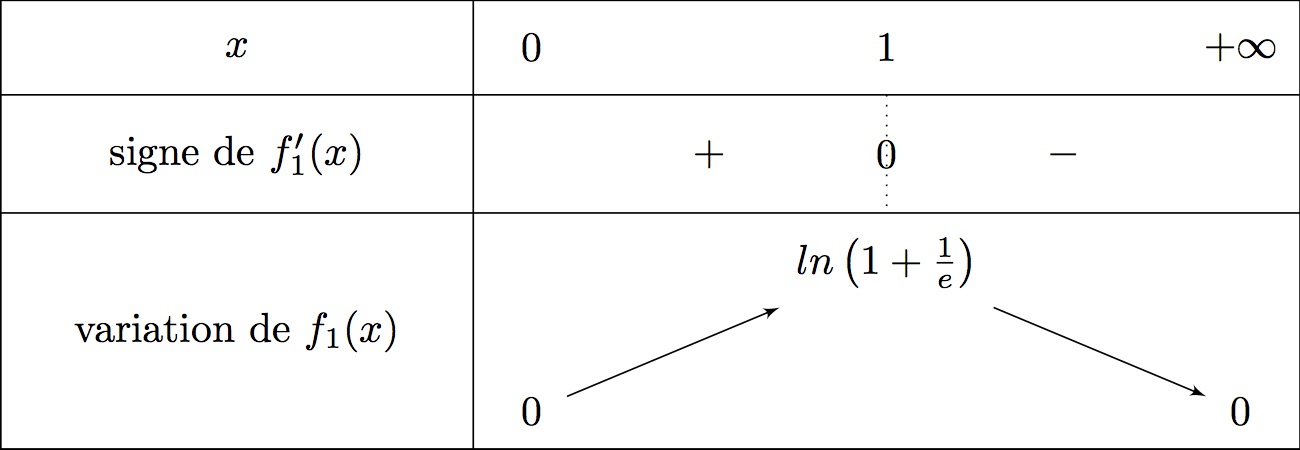
De plus,

De plus,
- donc
- donc
Question 6
Partie C : Etude et propriétés des fonctions
Montrer que pour tout réel appartenant à l'intervalle , .
En déduire la limite de en .
En déduire la limite de en .
Correction
équivaut successivement à
Or, ainsi : .
On pose et
Finalement, par composition : .
Autrement dit :
La courbe admet une asymptote horizontale d'équation au voisinage de plus l'infini.
Or, ainsi : .
On pose et
Finalement, par composition : .
Autrement dit :
La courbe admet une asymptote horizontale d'équation au voisinage de plus l'infini.
Question 7
Calculer pour tout réel appartenant à l'intervalle et en déduire le sens de variation de la fonction .
Correction
La fonction est dérivable sur et :
équivaut successivement à
Pour tout réel strictement positif et pour tout réel , le dénominateur est strictement positif.
Le signe de est alors du signe de .
Or,
Il vient alors que :
la fonction est donc positive sur et négative sur .
Finalement, la fonction est donc croissante sur et décroissante sur ..
On en déduit le tableau de variation de .
On a ci-dessous :
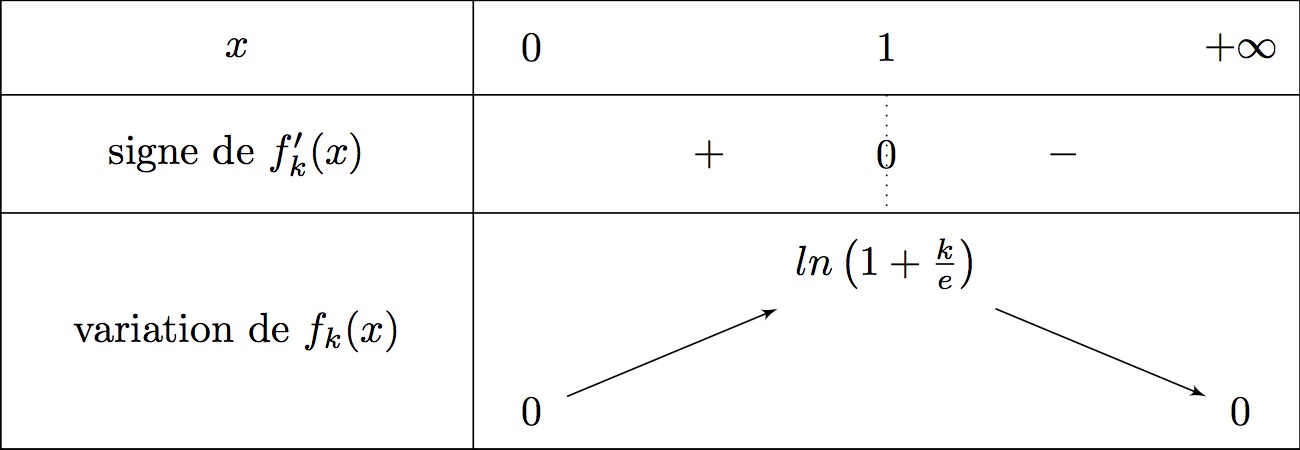
De plus,
équivaut successivement à
Pour tout réel strictement positif et pour tout réel , le dénominateur est strictement positif.
Le signe de est alors du signe de .
Or,
Il vient alors que :
la fonction est donc positive sur et négative sur .
Finalement, la fonction est donc croissante sur et décroissante sur ..
On en déduit le tableau de variation de .
On a ci-dessous :

De plus,
- donc
- donc
Question 8
Montrer que pour tout réel appartenant à l'intervalle , on a .
Correction
Pour tout réel appartenant à l'intervalle , on pose la fonction .
Ainsi est dérivable sur , il vient alors que :
. Donc le signe de est le même que celui de .
On a vu à la question , que la fonction est donc positive sur et négative sur .
Ainsi, la fonction est donc positive sur et négative sur .
On en déduit le tableau de variation de .
On a ci-dessous :
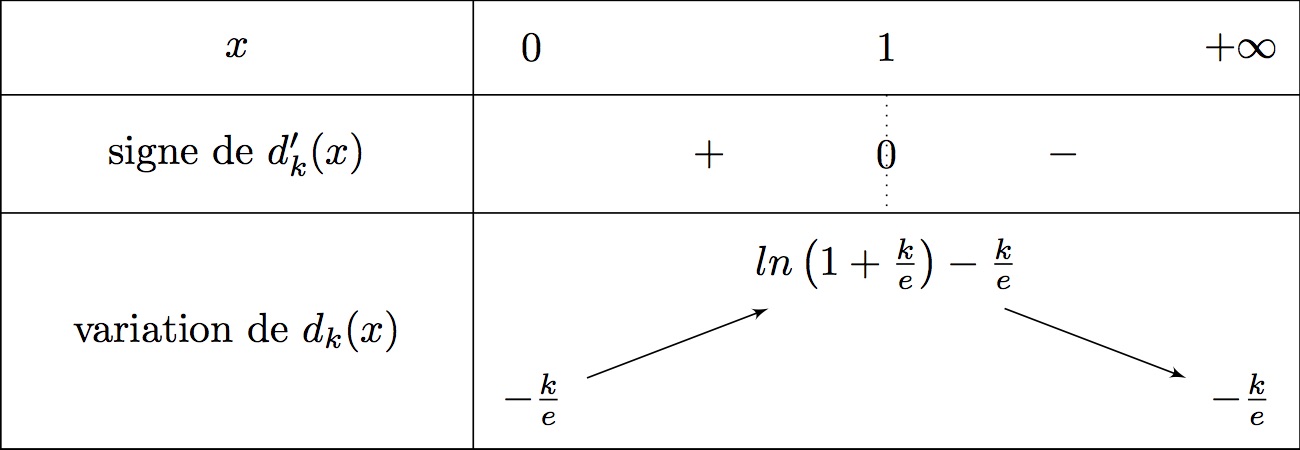
De plus,
Or , d'après la question pour tout réel positif ou nul .
Ainsi :
Autrement dit .
Finalement, pour tout réel positif ou nul, on peut affirmer que .
Autrement dit, alors .
Ainsi est dérivable sur , il vient alors que :
. Donc le signe de est le même que celui de .
On a vu à la question , que la fonction est donc positive sur et négative sur .
Ainsi, la fonction est donc positive sur et négative sur .
On en déduit le tableau de variation de .
On a ci-dessous :

De plus,
- car .
- On sait que d'où .
Or , d'après la question pour tout réel positif ou nul .
Ainsi :
Autrement dit .
Finalement, pour tout réel positif ou nul, on peut affirmer que .
Autrement dit, alors .
Question 9
Déterminer une équation de la tangente à au point O.
Correction
On sait que la formule de l'équation de la tangente au point d'abscisse 0 est :
D'une part :
donc
D'autre part :
alors
Ainsi :
Enfin :
D'une part :
donc
D'autre part :
alors
Ainsi :
Enfin :
Question 10
Soit et deux réels strictement positifs tels que .
Etudier la position relative de et .
Etudier la position relative de et .
Correction
On sait que .
Calculons tout d'abord .
équivaut successivement à
Maintenant étudions le signe de équivaut successivement à
équivaut successivement à
. Or donc . Ainsi
Finalement, pour tout réel , on a montré que . Ainsi .
La courbe est au-dessus de la courbe .
Calculons tout d'abord .
équivaut successivement à
Maintenant étudions le signe de équivaut successivement à
équivaut successivement à
. Or donc . Ainsi
Finalement, pour tout réel , on a montré que . Ainsi .
La courbe est au-dessus de la courbe .
Question 11
Partie D : Majoration d'une intégrale
Soit un réel strictement positif, on note l'aire, en unités d'aire, du domaine délimité par l'axe des abscisses, la courbe et les droites d'équation et .
Soit un réel strictement positif, on note l'aire, en unités d'aire, du domaine délimité par l'axe des abscisses, la courbe et les droites d'équation et .
Sans calculer , montrer que (on pourra utiliser le résultat de la question préliminaire).
Correction
Comme la fonction est positive et continue sur alors .
Pour et que alors .
On peut donc affirmer que d'après la question 2.
Donc .
De plus , les fonctions et sont continues sur et comme alors .
Finalement :
Pour et que alors .
On peut donc affirmer que d'après la question 2.
Donc .
De plus , les fonctions et sont continues sur et comme alors .
Finalement :
Question 12
On admet que est une primitive de la fonction .
Calculer alors .
Calculer alors .
Correction
Question 13
On admet que admet une limite en .
Montrer que .
Montrer que .
Correction
Comme alors
Or
Ainsi .
Nous avons d'une part : et d'autre part : alors
Or
Ainsi .
Nous avons d'une part : et d'autre part : alors