La fonction logarithme
Exercice 5 - Exercice 1
1 min
0
Le plan est rapporté à un repère orthonormal .
Question 1
Partie A
Soit la fonction définie sur par .
Soit la courbe représentative de et soit celle de la fonction définie sur par .
Soit la fonction définie sur par .
Soit la courbe représentative de et soit celle de la fonction définie sur par .
Déterminer les limites de en et en .
En déduire que a deux asymptotes que l'on déterminera.
En déduire que a deux asymptotes que l'on déterminera.
Correction
Calcul de la limite en 0 :
qui peut également s'écrire
par produit .
On en déduit que la courbe admet une asymptote verticale d'équation .
Calcul de la limite en :
qui peut également s'écrire
par somme .
On en déduit que la courbe admet une asymptote horizontale d'équation .
qui peut également s'écrire
par produit .
On en déduit que la courbe admet une asymptote verticale d'équation .
Calcul de la limite en :
qui peut également s'écrire
par somme .
On en déduit que la courbe admet une asymptote horizontale d'équation .
Question 2
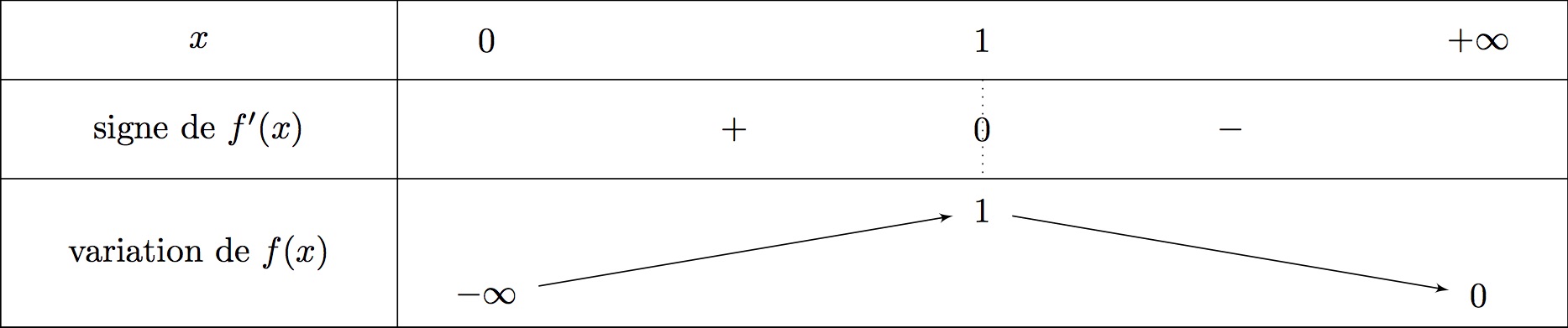
Calculer la dérivée de et étudier les variations de .
Correction
est dérivable sur .
On reconnait la forme avec et .
Ainsi et .
Il vient alors que :
Comme alors .
Donc est du signe de .
Or,
équivaut successivement à
Cela signifie que si et si .
On traduit ces informations dans le tableau de variation de la fonction .
Il vient alors que
 De plus :
De plus :
On reconnait la forme avec et .
Ainsi et .
Il vient alors que :
Comme alors .
Donc est du signe de .
Or,
équivaut successivement à
Cela signifie que si et si .
On traduit ces informations dans le tableau de variation de la fonction .
Il vient alors que

Question 3
Soit le point d'intersection de avec l'axe des abscisses.
Déterminer les coordonnées de .
Déterminer les coordonnées de .
Correction
Il faut résoudre l'équation .
équivaut successivement à
Comme alors
Les coordonnées du point d'intersection de avec l'axe des abscisses sont données par le point
équivaut successivement à
Comme alors
Les coordonnées du point d'intersection de avec l'axe des abscisses sont données par le point
Question 4
Pour tout de , on pose
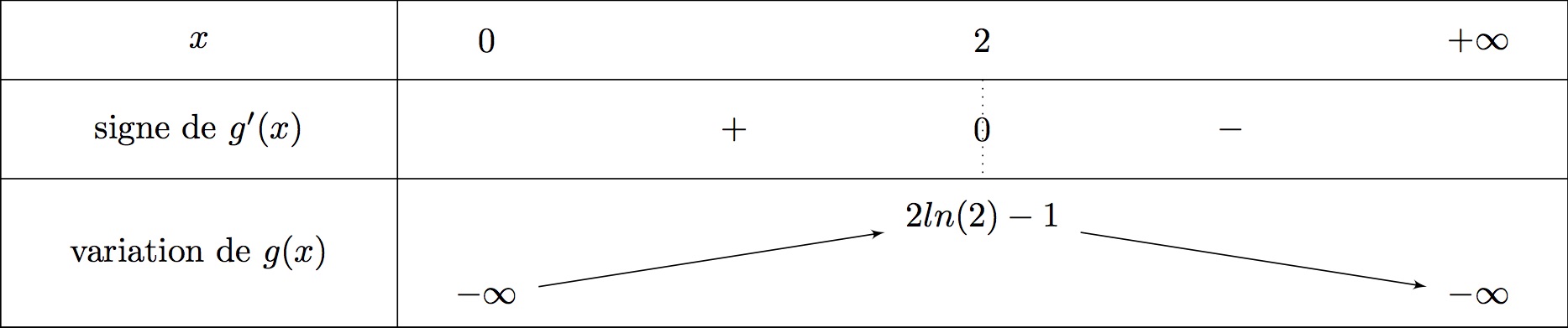
Etudier les variations de la fonction .
Dresser le tableau de variation complet.
Dresser le tableau de variation complet.
Correction
est dérivable sur .
Comme alors est du signe de .
Or,
Cela signifie que si et si .
On traduit ces informations dans le tableau de variation de la fonction .
Il vient alors que :
Calculons les limites de la fonction en 0 et en .
Calcul de la limite en 0 :
par produit . On en déduit que la courbe admet une asymptote verticale d'équation .
Calcul de la limite en :=
par produit .
Enfin, on calcule la valeur du maximum de qui est atteint quand .
et
Pour étudier le signe de correctement il faut tout mettre au même dénominateur
Comme alors est du signe de .
Or,
Cela signifie que si et si .
On traduit ces informations dans le tableau de variation de la fonction .
Il vient alors que :

Calculons les limites de la fonction en 0 et en .
Calcul de la limite en 0 :
par produit . On en déduit que la courbe admet une asymptote verticale d'équation .
Calcul de la limite en :=
On a factorisé par car on avait une forme indéterminée.
par produit .
Enfin, on calcule la valeur du maximum de qui est atteint quand .
et
Question 5
Montrer que l'équation admet une solution unique dans chacun des intervalles et .
Soit la solution appartenant .
Donner un encadrement de d'amplitude .
Soit la solution appartenant .
Donner un encadrement de d'amplitude .
Correction
On redonne le tableau de variation de .
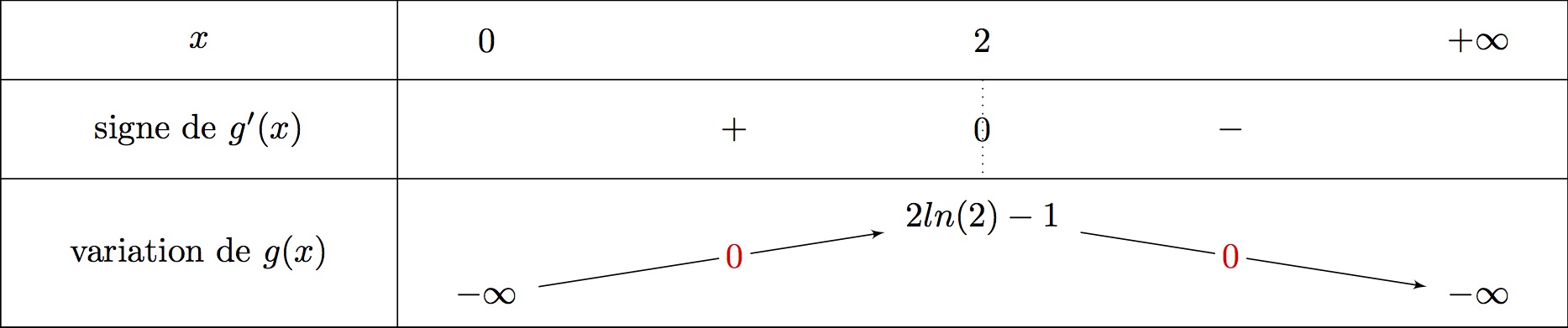
1er cas : L'unique solution sur l'intervalle
Sur , la fonction est continue et strictement croissante.
De plus, et . Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que .
On vérifie facilement que .
2ème cas : L'unique solution sur l'intervalle
Sur , la fonction est continue et strictement décroissante.
De plus, et . Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que .
A la calculatrice, on vérifie que :
et .
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que

1er cas : L'unique solution sur l'intervalle
Sur , la fonction est continue et strictement croissante.
De plus, et . Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que .
On vérifie facilement que .
2ème cas : L'unique solution sur l'intervalle
Sur , la fonction est continue et strictement décroissante.
De plus, et . Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que .
A la calculatrice, on vérifie que :
et .
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que
Question 6
En déduire le signe de sur .
Correction
- sur
- sur
- sur
On résume cela dans un tableau de signe

Question 7
Montrer que et en déduire que et se coupent en deux points
Correction
équivaut successivement à
Les abscisses des points communs à et à vérifient autrement dit .
Il en résulte donc que :
Donc :
équivaut successivement à
.
D'après la question précédente, les solutions de cette équation sont et .
Les abscisses des points communs à et à vérifient autrement dit .
Il en résulte donc que :
Donc :
équivaut successivement à
.
D'après la question précédente, les solutions de cette équation sont et .
Question 8
En déduire que sur , on a
Correction
Comme alors à le même signe que .
On rappelle que .
Ainsi à le même signe que car .
D'après la question , on a :
 Donc :
Donc :
 Il en résulte donc que sur l'intervalle , on a
Il en résulte donc que sur l'intervalle , on a
On rappelle que .
Ainsi à le même signe que car .
D'après la question , on a :


Question 9
Partie B
Soit la partie du plan définie par les inégalités suivantes :
où est le réel défini dans la partie A.
Soit la partie du plan définie par les inégalités suivantes :
où est le réel défini dans la partie A.
Déterminer l'aire de , notée , en unités d'aire .
On admet qu'une primitive de est .
On admet qu'une primitive de est .
Correction
Sur , est positive donc :
Question 10
Montrer que et donner une valeur approchée de à près.
Correction
D'après la question 5, on sait que donc que .
Ainsi .
Or,
On en déduit que :
On sait que :
équivaut successivement à
Finalement :
Ainsi .
Or,
On en déduit que :
On sait que :
équivaut successivement à
Finalement :
Question 11
Soit la suite définie pour supérieur ou égal à 1 par :
Montrer que, pour tout supérieur ou égal à , la double inégalité suivante est vraie :
Correction
Si sur alors
D'après la question , on a : sur l'intervalle donc également vrai sur car .Soit , en intégrant la double inégalité sur l'intervalle , on a
équivaut successivement à
Question 12
En déduire que la suite converge vers un réel que l'on déterminera.
Correction
Calculons d'une part : .
Pour cela on va utiliser les limites par composition.
On pose .
Ainsi
D'autre part :
D'après le théorème des gendarmes, on a :
La suite converge vers .
Pour cela on va utiliser les limites par composition.
On pose .
Ainsi
D'autre part :
D'après le théorème des gendarmes, on a :
La suite converge vers .
Question 13
Soit .
Calculer puis la limite de la suite .
Calculer puis la limite de la suite .
Correction
Relation de Chasles
Soient trois réels et appartenant à un intervalle , on a
Soient trois réels et appartenant à un intervalle , on a
équivaut successivement à
D'après la relation de Chasles, on a :
Or une primitive de est (question 9)
Or,
par somme
Question 14
Partie C
On considère, pour tout supérieur ou égal à 1, la fonction , définie sur par
On considère, pour tout supérieur ou égal à 1, la fonction , définie sur par
Calculer la dérivée de la fonction .
Correction
est dérivable sur comme quotient de fonction dérivable sur .
On reconnait la forme où et . Ainsi et .
Il en résulte que :
équivaut successivement à
On a factorisé par
On reconnait la forme où et . Ainsi et .
Il en résulte que :
équivaut successivement à
On a factorisé par
car
Question 15
Résoudre l'équation .
Soit la solution de cette équation.
Soit la solution de cette équation.
Correction
équivaut successivement à
. Or , d'où
Cette solution est notée
. Or , d'où
Cette solution est notée
Question 16
Déterminer la limite de la suite .
Correction
Pour cela on va utiliser les limites par composition.
Par composition :