La fonction logarithme
Exercice 2 - Exercice 1
1 min
0
Question 1
Partie A
Etude de fonction
On appelle la fonction définie sur l'intervalle par .
Etude de fonction
On appelle la fonction définie sur l'intervalle par .
Justifier que est strictement croissante sur l'intervalle .
Correction
est définie si donc est définie sur et est dérivable comme fonction composée de fonctions dérivables.
On calcule la dérivée de :
Or sur l'intervalle , le dénominateur et le numérateur .
Ainsi .
La fonction est donc croissante sur .
On calcule la dérivée de :
Or sur l'intervalle , le dénominateur et le numérateur .
Ainsi .
La fonction est donc croissante sur .
Question 2
Déterminer la limite de quand tend vers .
Correction
On a :
On pose , ainsi :
Il en résulte par composition que :
Finalement :
On pose , ainsi :
Il en résulte par composition que :
Finalement :
Question 3
On considère la fonction définie sur l'intervalle par .
On admettra que :
On admettra que :
Etudier les variations de sur .
Correction
équivaut successivement à
Ainsi .
Il en résulte donc que :
On traduit ces informations dans un tableau de variation
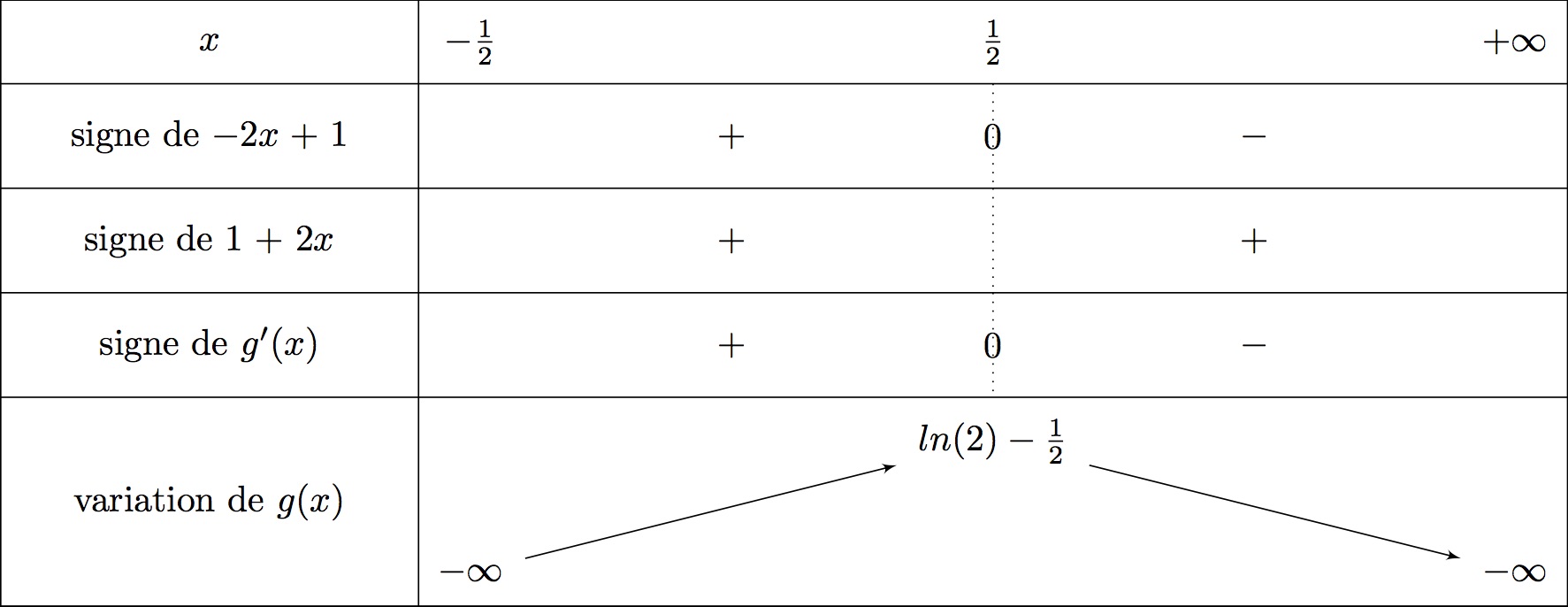 On a .
On a .
De plus : car
qui est du signe de puisque sur , .
Ainsi .
Il en résulte donc que :
- si alors et donc est croissante sur cet intervalle.
- si alors et donc est décroissante sur cet intervalle.
On traduit ces informations dans un tableau de variation

De plus : car
Question 4
Justifier que l'équation admet deux solutions 0 et une autre, notée , appartenant à l'intervalle .
Correction
- Sur , la fonction est continue et strictement croissante.
De plus, et .
Or .
En effet donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que . - Sur , la fonction est continue et strictement décroissante.
De plus, et . Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que .
De plus et .
Donc
Question 5
En déduire le signe de pour appartenant à l'intervalle .
Correction
D'après la question précédente, on en déduit le signe de :


Question 6
Justifier que pour tout réel appartenant à l'intervalle , appartient aussi à .
Correction
On a :
appartenant à l'intervalle qui se traduit en inégalité
Or la fonction est croissante sur , d'où :
Or : et.
On en déduit donc : .
Ainsi :
appartenant à l'intervalle qui se traduit en inégalité
Or la fonction est croissante sur , d'où :
Or : et.
On en déduit donc : .
Ainsi :
Question 7
Partie B
Etude d'une suite récurrente
Etude d'une suite récurrente
On appelle la suite définie par et .
Démontrer par récurrence que pour tout entier naturel , appartient à .
Démontrer par récurrence que pour tout entier naturel , appartient à .
Correction
Pour tout entier naturel , posons la propriété
Etape d'initialisation
On sait que ainsi car .
La propriété est vraie.
Etape d'hérédité
Soit un entier naturel.
On suppose qu'à partir d'un certain rang , la propriété est vraie c'est-à-dire : et vérifions si la propriété est également vraie au rang c'est-à-dire
Par hypothèse de récurrence :
, or la fonction est croissante , d'où
. Or et .
Il vient alors que :
. De plus,
Finalement :
Ainsi la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel , on a bien .
Etape d'initialisation
On sait que ainsi car .
La propriété est vraie.
Etape d'hérédité
Soit un entier naturel.
On suppose qu'à partir d'un certain rang , la propriété est vraie c'est-à-dire : et vérifions si la propriété est également vraie au rang c'est-à-dire
Par hypothèse de récurrence :
, or la fonction est croissante , d'où
. Or et .
Il vient alors que :
. De plus,
Finalement :
Ainsi la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel , on a bien .
Question 8
Démontrer par récurrence que la suite est croissante.
Correction
Pour tout entier naturel , posons la propriété
Etape d'initialisation
On sait que et que ainsi . Il vient alors que .
La propriété est vraie.
Etape d'hérédité
Soit un entier naturel.
On suppose qu'à partir d'un certain rang , la propriété est vraie c'est-à-dire et vérifions si la propriété est également vraie au rang c'est-à-dire
Par hypothèse de récurrence
, or la fonction est croissante , d'où
Finalement
Ainsi la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel , la suite est croissante.
Etape d'initialisation
On sait que et que ainsi . Il vient alors que .
La propriété est vraie.
Etape d'hérédité
Soit un entier naturel.
On suppose qu'à partir d'un certain rang , la propriété est vraie c'est-à-dire et vérifions si la propriété est également vraie au rang c'est-à-dire
Par hypothèse de récurrence
, or la fonction est croissante , d'où
Finalement
Ainsi la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel , la suite est croissante.
Question 9
Justifier que la suite est convergente.
Correction
La suite est majorée par et croissante elle converge donc vers un nombre inférieur ou égale à .