La fonction exponentielle
Exponentielle et suites - Exercice 1
35 min
50
Question 1
On considère la fonction définie sur par : .
Déterminer les limites de la fonction aux bornes de son domaine de définition. Que peut-on en déduire?
Correction
peut également s'écrire .
. Ici, il existe une asymptote horizontale d'équation au voisinage de .
Question 2
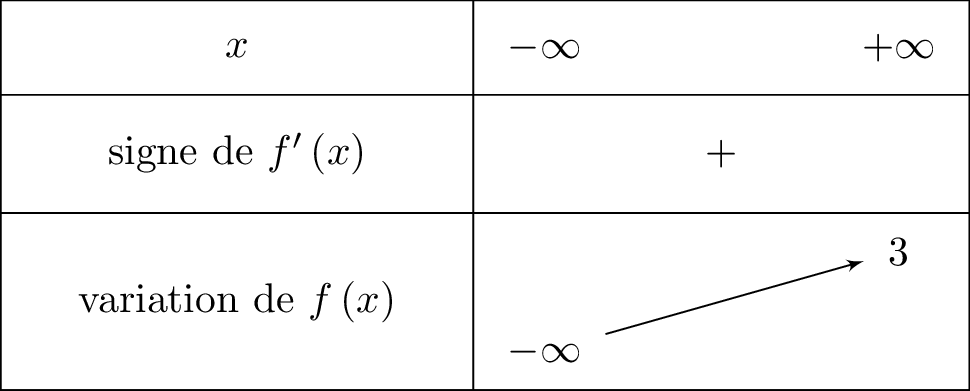
Etudier les variations de et dresser son tableau de variation.
Correction
Il vient alors que :
Or pour tout réel , on sait que . Ainsi :
Question 3
Montrer que pour tout réel , on a : .
Correction
Pour tout réel , on a :
Ainsi :
.
Or pour tout réel ,
Il en résulte que . D'où : ce qui nous permet de dire que .
Ainsi :
.
Or pour tout réel ,
Il en résulte que . D'où : ce qui nous permet de dire que .
Question 4
On considère la suite numérique est définie par et .
Calculer et .
Correction
ce qui donne ainsi :
ce qui donne :
Question 5
Montrer que pour tout entier naturel , on a :
Correction
Pour tout entier naturel , posons la propriété
Etape d'initialisation
On a vu précédemment que . Donc on a bien :
La propriété est vraie.
Etape d'hérédité
Soit un entier naturel.
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire : et vérifions si la propriété est également vraie au rang c'est-à-dire :
Par hypothèse de récurrence,
, or une fonction strictement croissante sur , ainsi :
Puisque et
Il vient alors que :
. Or . Ce qui donne :
Finalement :
Ainsi la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel :
Etape d'initialisation
On a vu précédemment que . Donc on a bien :
La propriété est vraie.
Etape d'hérédité
Soit un entier naturel.
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire : et vérifions si la propriété est également vraie au rang c'est-à-dire :
Par hypothèse de récurrence,
, or une fonction strictement croissante sur , ainsi :
Puisque et
Il vient alors que :
. Or . Ce qui donne :
Finalement :
Ainsi la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel :
Question 6
Etudier la monotonie de la suite .
Correction
Une suite est croissante si et seulement : autrement dit .
D'après la question , on sait que : et
On remarque que .
On conjecture que la suite est croissante.
Il faut donc démontrer cette conjecture par récurrence
Pour tout entier naturel , posons la propriété
Etape d'initialisation
On a vu précédemment que .
La propriété est vraie.
Etape d'hérédité
Soit un entier naturel.
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire : et vérifions si la propriété est également vraie au rang c'est-à-dire :
Par hypothèse de récurrence,
, or une fonction strictement croissante sur , ainsi :
. Or . Ce qui donne :
Ainsi la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel , la suite est croissante.
D'après la question , on sait que : et
On remarque que .
On conjecture que la suite est croissante.
Il faut donc démontrer cette conjecture par récurrence
Pour tout entier naturel , posons la propriété
Etape d'initialisation
On a vu précédemment que .
La propriété est vraie.
Etape d'hérédité
Soit un entier naturel.
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire : et vérifions si la propriété est également vraie au rang c'est-à-dire :
Par hypothèse de récurrence,
, or une fonction strictement croissante sur , ainsi :
. Or . Ce qui donne :
Ainsi la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel , la suite est croissante.
Question 7
Que peut-on en déduire?
Correction
- Une suite décroissante et minorée est convergente, elle admet donc une limite finie.
- Une suite croissante et majorée est convergente, elle admet donc une limite finie.