La fonction exponentielle
Exercices types : 4ème partie - Exercice 1
1 h 10 min
100
Partie A : Etude d'une fonction auxiliaire.
Question 1
On considère la fonction définie sur par
Déterminer la limite de en .
Correction
par produit
Finalement :
Finalement :
Question 2
Démontrer que la limite de en vaut .
Correction
Il s'agit d'une forme indéterminée .
Nous allons donc développer l'expression de et la transformer afin de relever la forme indéterminée.
. On rappelle que .
Ainsi : donc
D'où :
par somme
Finalement :
Nous allons donc développer l'expression de et la transformer afin de relever la forme indéterminée.
. On rappelle que .
D'où :
par somme
Finalement :
Question 3
On admet que la fonction est dérivable sur et on note sa dérivée.
Calculer pour tout réel puis dresser le tableau de variation de .
Correction
Soit tel que soit dérivable sur .
Ici on reconnait la forme : avec ; et
Ainsi : ; et .
Il vient alors que :
Pour tout réel , on vérifie aisément . Le signe de dépend alors de . Il vient que :
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera supérieur ou égale à .
On en déduit le tableau de variation suivant :
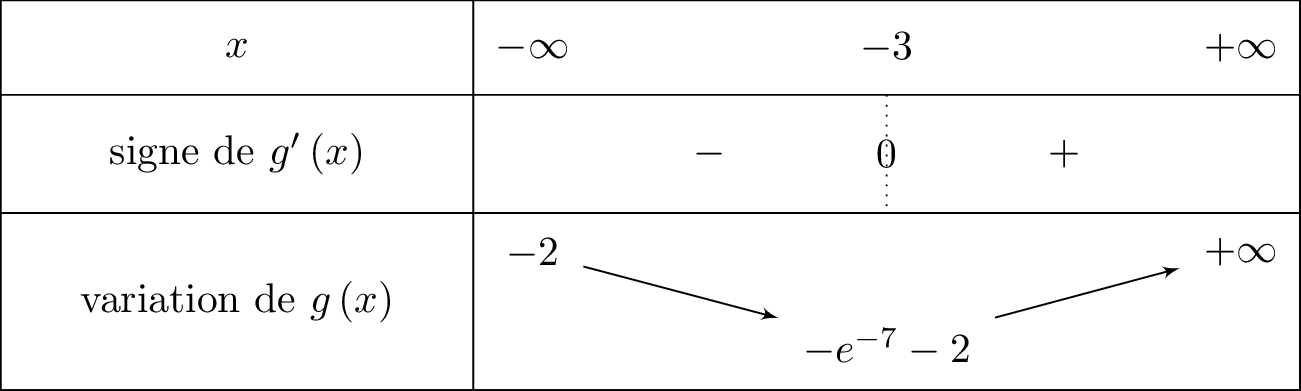
d'où :
Ici on reconnait la forme : avec ; et
Ainsi : ; et .
Il vient alors que :
Pour tout réel , on vérifie aisément . Le signe de dépend alors de . Il vient que :
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera supérieur ou égale à .
On en déduit le tableau de variation suivant :

Question 4
Démontrer que l’équation admet une unique solution sur .
Correction
Nous allons faire apparaitre le zéro dans le tableau de variation. On a donc :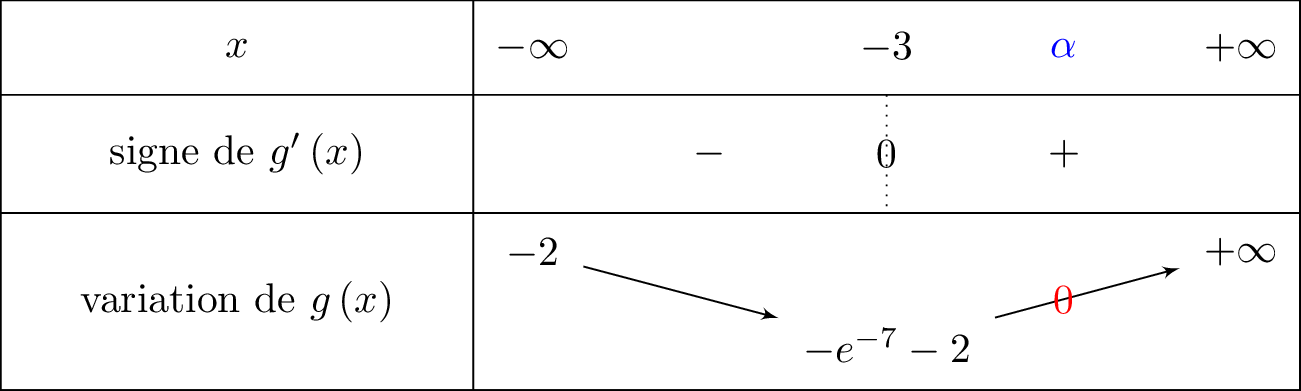

- Sur , la fonction est continue et admet comme minimum.
La fonction est strictement négative.
Donc l'équation n'a pas de solution sur cet intervalle. - Sur , la fonction est continue et strictement croissante.
De plus, et
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que .
Question 5
En déduire le signe de la fonction sur .
Correction

Sur , la fonction est continue et strictement croissante et
Donc pour tout et pour tout
On résume cela dans un tableau de signe :
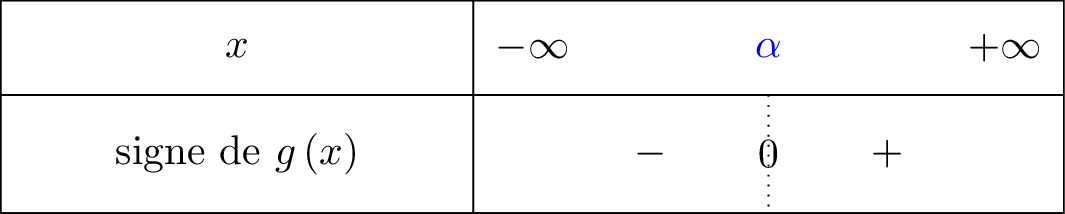
Question 6
À l’aide de la calculatrice, donner un encadrement d’amplitude de .
Correction
A la calculatrice, on vérifie que :
et
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
et
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
Question 7
Partie B : Étude de la fonction .
Soit la fonction définie sur par .
Soit la fonction définie sur par .
Résoudre l’équation sur .
Correction
.
Il s'agit donc d'une équation produit nul :
Ainsi : ou .
D'une part :
D'autre part :
L’équation a deux solutions :
Il s'agit donc d'une équation produit nul :
Ainsi : ou .
D'une part :
D'autre part :
L’équation a deux solutions :
Question 8
On admet que la fonction est dérivable sur et on note sa fonction dérivée.
On admet par ailleurs que, pour tout réel , où la fonction est celle définie à la partie A .
On admet enfin que et que
On admet par ailleurs que, pour tout réel , où la fonction est celle définie à la partie A .
On admet enfin que et que
Étudier les variations de la fonction sur . On ne demande pas de calculer les limites de aux bornes du domaine de définition.
Correction
L'énoncé, nous indique que . Nous connaissons le signe de obtenue à la question que l'on rappelle ci-dessous.
 Donc le signe de dépend alors de .
Donc le signe de dépend alors de .
Il vient alors que :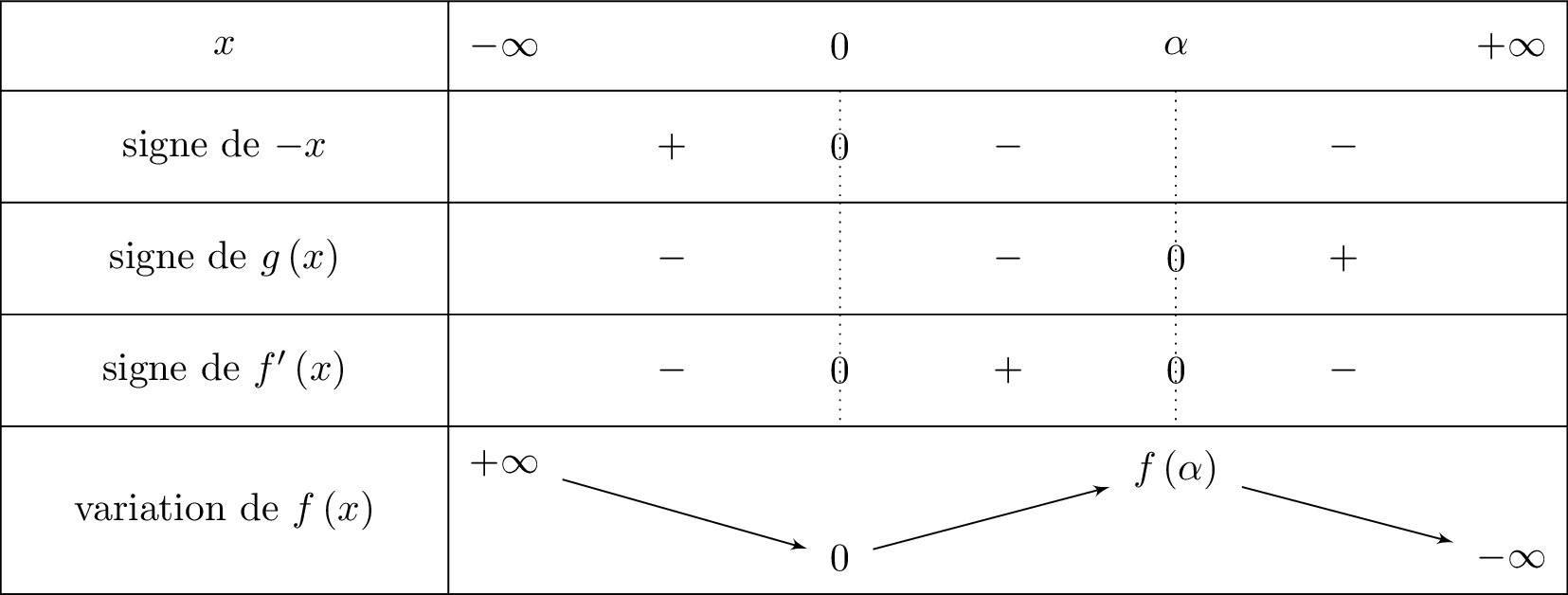
d'où :

Il vient alors que :

Question 9
Démontrer que le maximum de la fonction sur est égal à .
Correction
D'après le tableau de variation de la question , le maximum est atteint pour la valeur . Il nous faut donc calculer .
 Nous savons tout d'abord , d'après la question que . Ainsi :
Nous savons tout d'abord , d'après la question que . Ainsi :
De plus :
or . Nous remplaçons, cela donne :
. Nous avons tout mis au même dénominateur .

De plus :
or . Nous remplaçons, cela donne :
. Nous avons tout mis au même dénominateur .
Question 10
Partie C : Aire d’un domaine. Dans un repère orthonormé , on note le domaine compris entre la courbe représentative de la fonction , la parabole d’équation et les droites d’équations et .
Déterminer la position relative des courbes et .
Correction
La position relative entre deux courbes étudie les intervalles sur lesquelles une des courbes est supérieure à l'autre.
Pour étudier la position relative entre et , il faut étudier le signe de .
Nous allons introduire une fonction tel que : Pour étudier la position relative entre et , il faut étudier le signe de .
Ainsi :
équivaut successivement à :
Cette fonction produit de deux fonctions positives est positive et ne s’annule que pour . Géométriquement ceci montre que la parabole est au dessus de la courbe , le seul point commun étant l’origine.
Question 11
On admet qu’une primitive de la fonction sur est définie par :
Calculer l’aire du domaine en unité d’aire. On donnera la valeur exacte.
Correction
D'après la question précédente, nous savons que sur l’intervalle la courbe est au dessus de la courbe , donc l’aire de la surface limitée par la courbe , la courbe et les droites d’équation et , est en unité d’aire égale à l’intégrale :
unité d’aire