La fonction exponentielle
Exercices types : 3ème partie - Exercice 1
30 min
50
Lorsque la queue d’un lézard des murailles casse, elle repousse toute seule en une soixantaine de jours. Lors de la repousse, on modélise la longueur en centimètre de la queue du lézard en fonction du nombre de jours. Cette longueur est modélisée par la fonction définie sur par :
où est la fonction définie sur par :
où est la fonction définie sur par :
Question 1
On admet que la fonction est dérivable sur et on note sa fonction dérivée.
Vérifier que pour tout positif on a : .
En déduire le sens de variations de la fonction sur .
En déduire le sens de variations de la fonction sur .
Correction
Comme alors c'est à dire .
Maintenant nous allons calculer la dérivée de .
Nous savons que ainsi
Soit :
. Or :
Finalement :
De plus, pour tout , comme alors . Ainsi : et de ce fait . Enfin , .
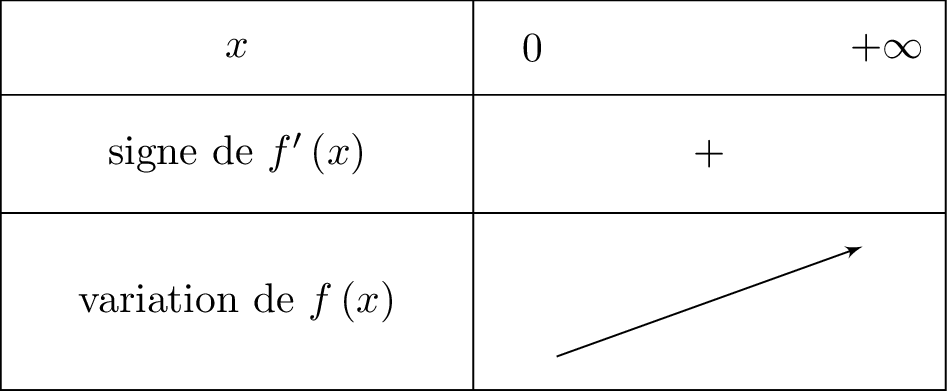
Il en résulte donc que pour tout , est strictement positive .
La fonction est alors strictement croissante sur .
Question 2
Calculer .
En déduire une estimation, arrondie au millimètre, de la longueur de la queue du lézard après vingt jours de repousse.
En déduire une estimation, arrondie au millimètre, de la longueur de la queue du lézard après vingt jours de repousse.
Correction
Après jours de repousse, la taille de la queue du lézard sera environ de cm.
Question 3
Selon cette modélisation, la queue du lézard peut-elle mesurer cm?
Correction
Nous allons calculer la limite en .
On commence par calculer .
Or :
On pose .
Ainsi : .
Par composition :
Maintenant, il nous reste à calculer
Nous venons de voir que .
Nous posons
Ainsi : .
Par composition :
La fonction est strictement croissante et admet comme valeur maximale : la taille de la repousse ne sera jamais égale à cm.
On commence par calculer .
Or :
On pose .
Ainsi : .
Par composition :
Maintenant, il nous reste à calculer
Nous venons de voir que .
Nous posons
Ainsi : .
Par composition :
La fonction est strictement croissante et admet comme valeur maximale : la taille de la repousse ne sera jamais égale à cm.
Question 4
On souhaite déterminer au bout de combien de jours la vitesse de croissance est maximale. On admet que la vitesse de croissance au bout de jours est donnée par .
On admet que la fonction dérivée est dérivable sur , on note la fonction dérivée de et on admet que :
On admet que la fonction dérivée est dérivable sur , on note la fonction dérivée de et on admet que :
Déterminer les variations de sur .
Correction
D'après l'énoncé, nous savons que : .
Pour tout , nous vérifions aisément que et .
Il en résulte que le signe de dépend alors de .
D'après la question , nous avons vu que .
Nous allons maintenant déterminer sur quel intervalle et ensuite nous allons dresser le tableau de signe de .
Ainsi :
Finalement :
sur et sur . est donc croissante sur et décroissante sur .
Nous en déduisons le tableau de variation ci-dessous :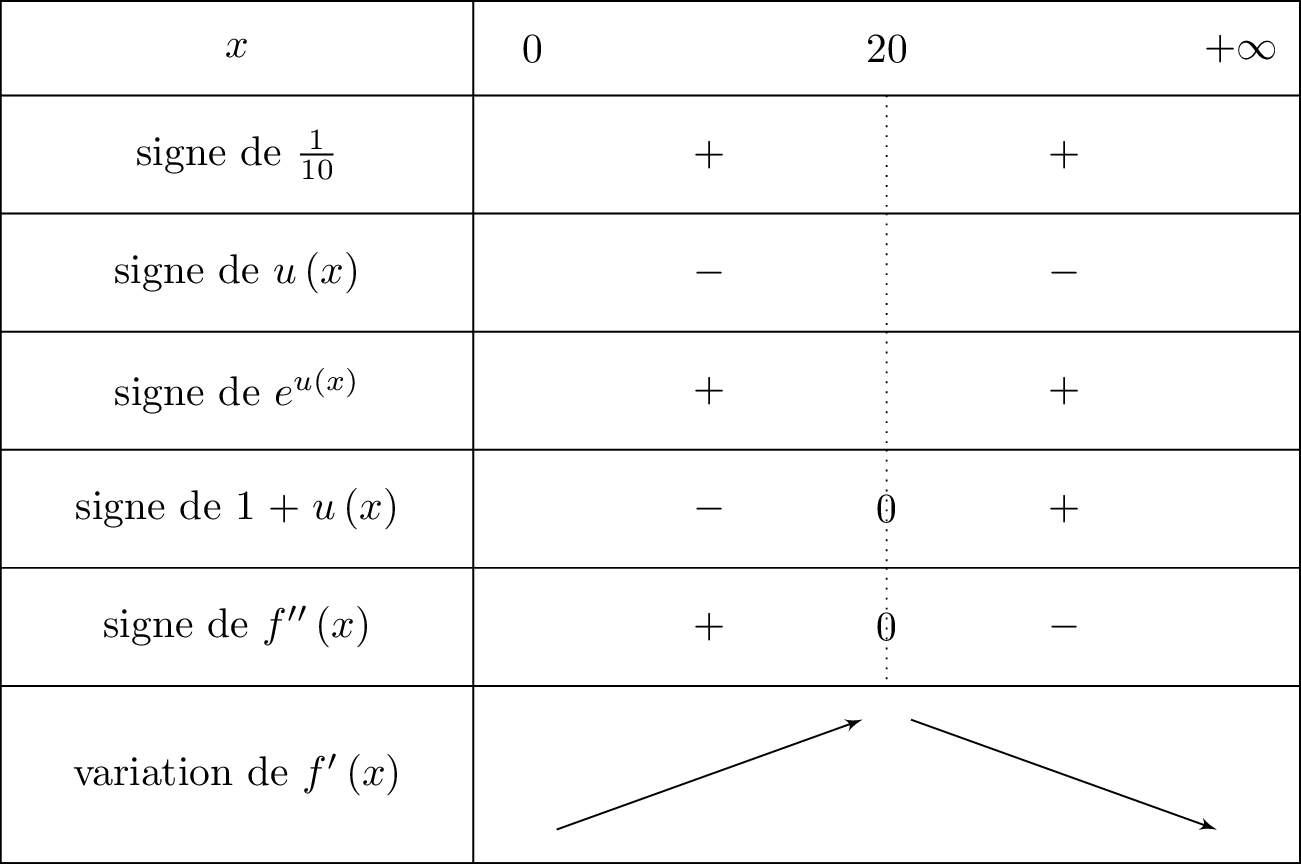
Pour tout , nous vérifions aisément que et .
Il en résulte que le signe de dépend alors de .
D'après la question , nous avons vu que .
Nous allons maintenant déterminer sur quel intervalle et ensuite nous allons dresser le tableau de signe de .
Ainsi :
Finalement :
sur et sur . est donc croissante sur et décroissante sur .
Nous en déduisons le tableau de variation ci-dessous :

Question 5
En déduire au bout de combien de jours la vitesse de croissance de la longueur de la queue du lézard est maximale.
Correction
D’après le résultat précédent la vitesse est maximale pour : la vitesse de croissance de la longueur de la queue du lézard est maximale au bout de jours.