La fonction exponentielle
Exercices types : 2ème partie - Exercice 1
50 min
75
Question 1
PARTIE A
On considère la fonction définie sur par
On considère la fonction définie sur par
Etudier le sens de variation de la fonction sur .
Correction
est dérivable sur .
On a :
Résolvons l'inéquation :
équivaut successivement à :
Cela signifie que lorsque . Nous traduisons cela dans un tableau de variation, ainsi :
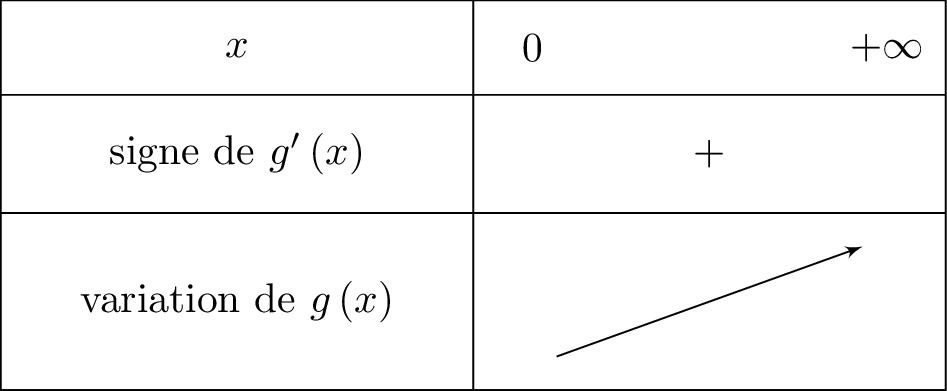
On a :
Résolvons l'inéquation :
équivaut successivement à :
Cela signifie que lorsque . Nous traduisons cela dans un tableau de variation, ainsi :

Question 2
Déterminer le signe de suivant les valeurs de .
Correction
On remarque que :
On indique cela dans le tableau de variation ci-dessous :
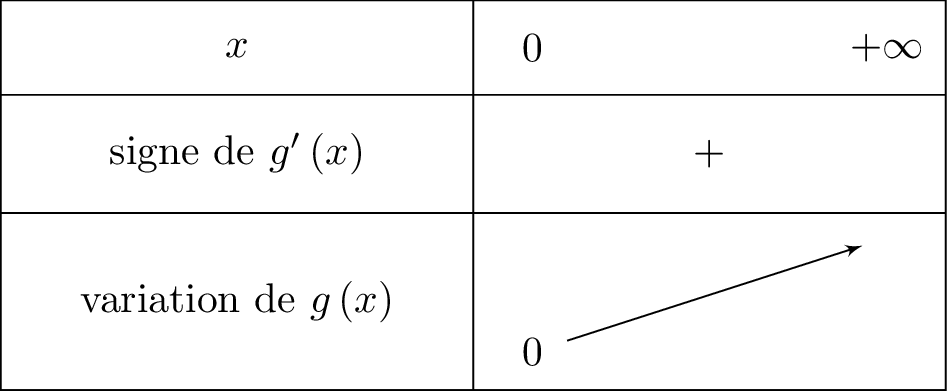 Ainsi la fonction admet un minimum qui vaut lorsque . La fonction est donc positive.
Ainsi la fonction admet un minimum qui vaut lorsque . La fonction est donc positive.
Ainsi, pour tout de l'intervalle , on a :
On indique cela dans le tableau de variation ci-dessous :

Ainsi, pour tout de l'intervalle , on a :
.
Question 3
En déduire que pour tout réel appartenant à l'intervalle , on a :
Correction
On a vu à la question , que pour tout de l'intervalle , on a :
Ainsi :
donc
D'où : . Ce qui permet de dire que tout réel appartenant à l'intervalle , on a :
Ainsi :
donc
D'où : . Ce qui permet de dire que tout réel appartenant à l'intervalle , on a :
Question 4
PARTIE B
On considère la fonction définie sur par : . On nomme la courbe représentative de la fonction .
On admet que est strictement croissante sur
On considère la fonction définie sur par : . On nomme la courbe représentative de la fonction .
On admet que est strictement croissante sur
Montrer que pour tout appartenant à , on a .
Correction
Dans l'exercice, on nous indique que la fonction est strictement croissante sur l'intervalle
Calculons et .
ce qui donne :
ce qui donne :
Nous dressons le tableau de variation de sur l'intervalle . Il vient alors que :
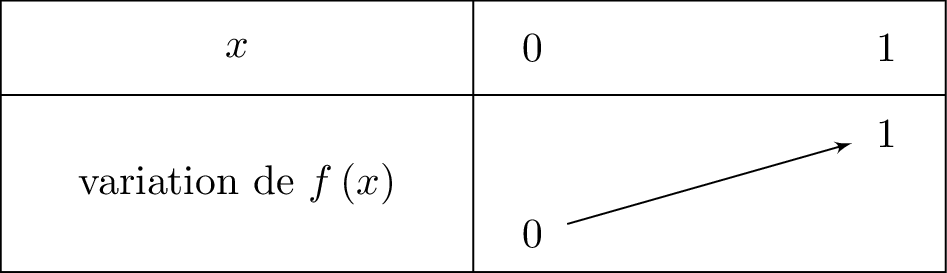 Il en résulte donc que pour tout appartenant à , on a
Il en résulte donc que pour tout appartenant à , on a
Calculons et .
ce qui donne :
ce qui donne :
Nous dressons le tableau de variation de sur l'intervalle . Il vient alors que :

Question 5
Soit la droite d'équation .
Montrer que pour tout appartenant à l'intervalle , on a :
Correction
équivaut successivement à :
. Nous avons tout mis au même dénominateur :
Maintenant développons l'expression :
équivaut successivement à :
Comme et que , il vient alors que :
. Nous avons tout mis au même dénominateur :
Maintenant développons l'expression :
équivaut successivement à :
Comme et que , il vient alors que :
Question 6
Etudier la position relative de la droite et de la courbe sur l'intervalle .
Correction
D'après la question précédente, on sait que :
Pour tout réel appartenant à l'intervalle , nous savons que :
d'après la question : d'après la question : Il en résulte donc que est alors du signe de .
Résolvons : équivalent à .
Il en résulte donc que :
lorsque lorsque Traduisons toutes ces données dans un tableau de signe pour .
 Il en résulte que pour tout réel appartenant à l'intervalle , on a :
Il en résulte que pour tout réel appartenant à l'intervalle , on a :
donc que .
Cela signifie que pour tout réel appartenant à l'intervalle , la courbe est au-dessus de la droite .
Pour tout réel appartenant à l'intervalle , nous savons que :
Résolvons : équivalent à .
Il en résulte donc que :

donc que .
Cela signifie que pour tout réel appartenant à l'intervalle , la courbe est au-dessus de la droite .
Question 7
PARTIE C.
On considère la suite est définie par et .
On considère la suite est définie par et .
Montrer, que pour tout entier naturel , on a :
Correction
Commençons, tout d’abord, par calculer .
ou encore Ainsi : .
Raisonnons par récurrence.
Pour tout entier naturel , posons la propriété
Etape d'initialisation
On a vu précédemment que .
On remarque que
La propriété est vraie.
Etape d'hérédité
Soit un entier naturel.
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire : et vérifions si la propriété est également vraie au rang c'est-à-dire : .
Par hypothèse de récurrence,
, or est une fonction croissante sur , ainsi :
. Comme alors : . Il vient alors que :
. Or : et .
D'où :
Il en résulte donc que :
Ainsi la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel : .
ou encore Ainsi : .
Raisonnons par récurrence.
Pour tout entier naturel , posons la propriété
Etape d'initialisation
On a vu précédemment que .
On remarque que
La propriété est vraie.
Etape d'hérédité
Soit un entier naturel.
On suppose qu'il existe un entier tel que la propriété soit vraie c'est-à-dire : et vérifions si la propriété est également vraie au rang c'est-à-dire : .
Par hypothèse de récurrence,
, or est une fonction croissante sur , ainsi :
. Comme alors : . Il vient alors que :
. Or : et .
D'où :
Il en résulte donc que :
Ainsi la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel : .
Question 8
En déduire que la suite est convergente et déterminer sa limite.
Correction
- Une suite décroissante et minorée est convergente, elle admet donc une limite finie.
- Une suite croissante et majorée est convergente, elle admet donc une limite finie.
Cela signifie que la suite est majorée par et que la suite est croissante car .
Il en résulte donc que la suite est convergente et que la suite admette une limite finie que l'on note .
Ainsi : et par unicité de la limite on a donc :
Or :
D'où : . Or est une fonction continue et par passage à la limite, on a :
. Il faut maintenant résoudre cette équation :
. Or d'après la question , on a : . Il en résulte que :
. Or , nous savons d'après la question que et ce qui implique que :
Ainsi :
La suite converge vers le réel .