La fonction exponentielle
Exercice 6 - Exercice 1
1 min
0
Question 1
Partie A
On considère la fonction définie sur par :
Et l'on désigne par sa courbe représentative dans un repère orthonormal
On considère la fonction définie sur par :
Et l'on désigne par sa courbe représentative dans un repère orthonormal
Calculer la limite de lorsque tend vers .
Que peut-on en déduire pour la courbe ?
Que peut-on en déduire pour la courbe ?
Correction
En écrivant pour ,
De plus,
Finalement, par somme, .
Géométriquement ce résultat montre que la droite dont une équation est est asymptote horizontale à au voisinage de plus l'infini.
De plus,
Finalement, par somme,
Géométriquement ce résultat montre que la droite dont une équation est est asymptote horizontale à au voisinage de plus l'infini.
Question 2
Calculer , en déduire les variations de pour appartenant à .
Correction
est dérivable sur .
On reconnait la forme avec et .
Ainsi et .
Il vient alors que :
Or pour tout réel on a et .
Ainsi :
est donc strictement croissante sur .
La valeur de son minimum est donnée par : .
On reconnait la forme avec et .
Ainsi et .
Il vient alors que :
Or pour tout réel on a et .
Ainsi :
est donc strictement croissante sur .
La valeur de son minimum est donnée par : .
Question 3
Déterminer une équation de la tangente à en son point d'abscisse .
Correction
On sait que la formule de l'équation de la tangente au point d'abscisse est :
D'une part :
alors
D'autre part :
alors
Ainsi :
Enfin :
D'une part :
alors
D'autre part :
alors
Ainsi :
Enfin :
Question 4
Montrer que l'équation admet une solution unique .
Montrer que appartient à et déterminer un encadrement d'amplitude de .
Montrer que appartient à et déterminer un encadrement d'amplitude de .
Correction
On commence par dresser le tableau de variation de la fonction .
D'où :
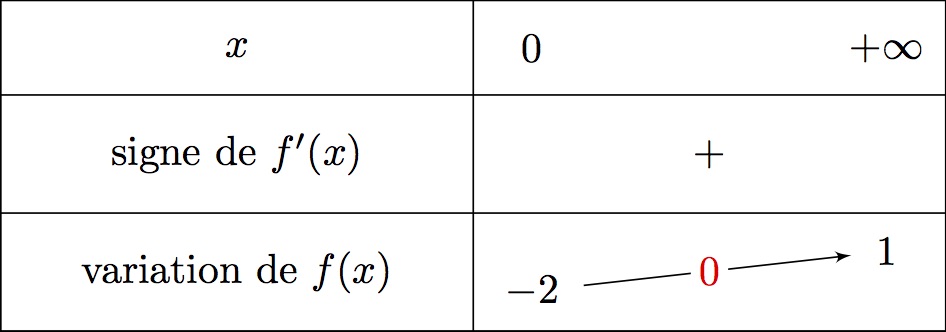
Sur , la fonction est continue et strictement croissante.
De plus, et .
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que .
La calculatrice donne et , donc .
D'où :
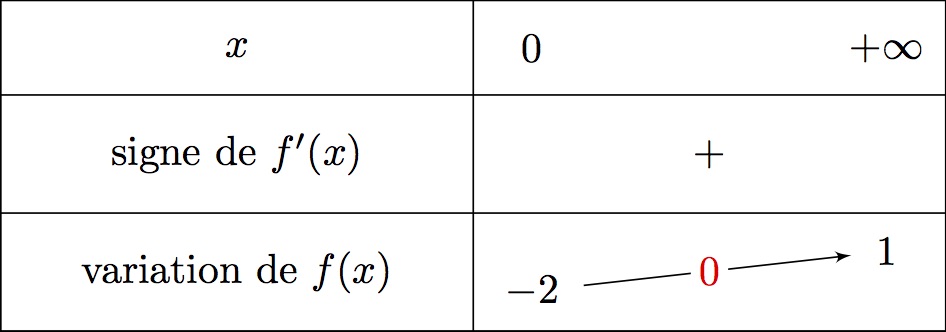
Sur , la fonction est continue et strictement croissante.
De plus, et .
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que .
La calculatrice donne et , donc .
Question 5
Déterminer les réels et tels que, pour tout , .
Correction
On a pour , de :
Or nous voulons que : ainsi :
Par identification, on obtient le système suivant :
d'où
Finalement :
Or nous voulons que : ainsi :
Par identification, on obtient le système suivant :
d'où
Finalement :
Question 6
En déduire l'aire du domaine plan limité par , et la droite d'équation (on admettra que est au-dessus de ).
Correction
étant au-dessus de , l'aire, en unité d'aire de la surface est égale à l'intégrale :
Question 7
Partie B
Soit un entier naturel non nul.
On considère la fonction définie sur par :
Soit un entier naturel non nul.
On considère la fonction définie sur par :
Calculer et donner son signe sur .
Préciser et .
Dresser le tableau de variation de .
Préciser et .
Dresser le tableau de variation de .
Correction
est dérivable sur .
On reconnait la forme avec et .
Ainsi et .
Il vient alors que :
Or pour tout réel on a et .
Ainsi :
est donc strictement croissante sur .
La valeur de son minimum est donnée par : .
Or quel que soit , , car pour (on a factorisé par )
D'autre part , on a donc par somme.
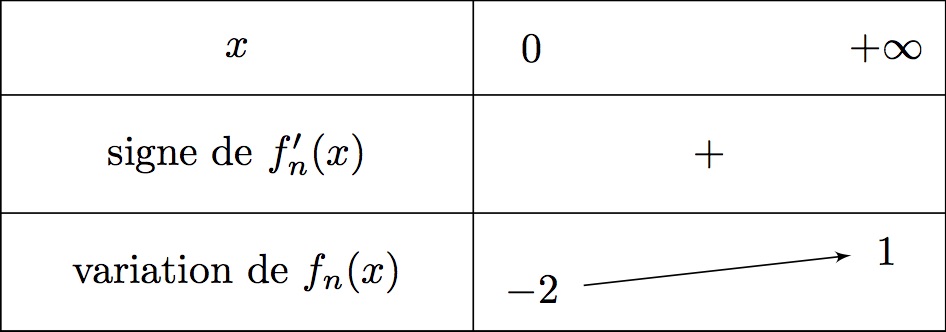
On reconnait la forme avec et .
Ainsi et .
Il vient alors que :
Or pour tout réel on a et .
Ainsi :
est donc strictement croissante sur .
La valeur de son minimum est donnée par : .
Or quel que soit , , car pour (on a factorisé par )
D'autre part , on a donc par somme.
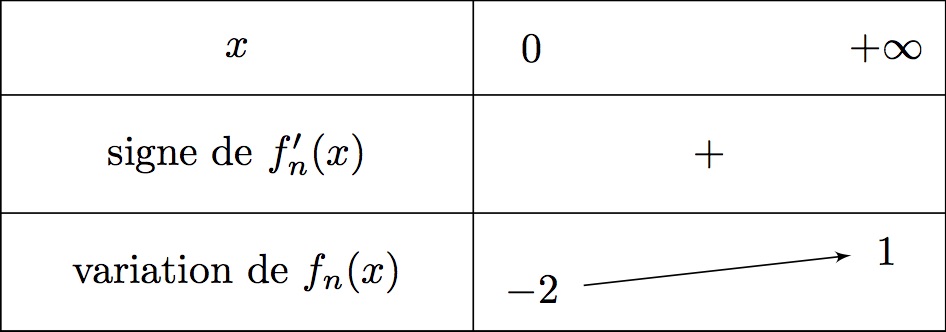
Question 8
Calculer .
Quel est son signe ?
Quel est son signe ?
Correction
d'où
Ainsi : car quel que soit , .
Ainsi : car quel que soit , .
Question 9
Calculez .
Correction
Question 10
Démontrer, par récurrence que, pour tout de , .
Correction
Pour tout entier naturel , posons la propriété
Etape d'initialisation
Lorsque , on a qui donne .
La propriété est vraie.
Etape d'hérédité
Soit un entier naturel.
On suppose qu'à partir d'un certain rang , la propriété est vraie c'est-à-dire et vérifions si la propriété est également vraie au rang c'est-à-dire ou encore
Par hypothèse de récurrence
, d'où en multipliant chaque membre par :
Or vérifions si
(1)
Or .
L'inégalité (1) est donc vraie pour , donc aussi.
Ainsi la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel , on a bien .
Etape d'initialisation
Lorsque , on a qui donne .
La propriété est vraie.
Etape d'hérédité
Soit un entier naturel.
On suppose qu'à partir d'un certain rang , la propriété est vraie c'est-à-dire et vérifions si la propriété est également vraie au rang c'est-à-dire ou encore
Par hypothèse de récurrence
, d'où en multipliant chaque membre par :
Or vérifions si
(1)
Or .
L'inégalité (1) est donc vraie pour , donc aussi.
Ainsi la propriété est vraie.
Conclusion
Puisque la propriété est vraie et que nous avons prouvé l'hérédité, on peut en déduire, par le principe de récurrence que pour tout entier naturel , on a vraie, c'est à dire que pour tout entier naturel , on a bien .
Question 11
En déduire le signe de .
Correction
Comme et que alors
Question 12
Montrer que l'équation admet une solution unique sur ; cette solution sera notée .
Correction
Sur , la fonction est continue et strictement croissante.
De plus, et .
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution tel que .
De plus, et .
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution tel que .
Question 13
Calculer puis .
Correction
On sait que c'est-à-dire que .
Comme et que , d'après le théorème de comparaison .
De plus, pour ,
Comme , d'après le théorème des « gendarmes », .
Comme et que , d'après le théorème de comparaison .
De plus, pour ,
Comme , d'après le théorème des « gendarmes »,
Question 14
En remarquant que, pour tout de : , montrer que la valeur moyenne, de sur est égale à :
Correction
Commençons par vérifier que :
La valeur moyenne de sur est égale à :
La valeur moyenne de sur est égale à :
Une primitive de est car une primitive de est