La fonction exponentielle
Exercice 5 - Exercice 1
1 min
0
Le plan est muni d'un repère orthonormal .
Pour tout entier naturel , on considère la fonction définie sur par :
On désigne par la courbe représentative de dans le repère .
Pour tout entier naturel , on considère la fonction définie sur par :
On désigne par la courbe représentative de dans le repère .
Question 1
Partie A
Dans cette partie, on s'intéresse seulement à la fonction correspondant respectivement à .
Dans cette partie, on s'intéresse seulement à la fonction correspondant respectivement à .
Déterminer la limite de quand tend vers .
Que peut-on en déduire graphiquement ?
Que peut-on en déduire graphiquement ?
Correction
alors : .
par quotient
La courbe admet une asymptote horizontale d'équation au voisinage de moins l'infini.
par quotient
La courbe admet une asymptote horizontale d'équation au voisinage de moins l'infini.
Question 2
Déterminer la limite de quand tend vers .
Que peut-on en déduire graphiquement ?
Que peut-on en déduire graphiquement ?
Correction
On a : .
On rencontre une forme indéterminée.
On va donc factoriser le numérateur et le dénominateur par .
par quotient
La courbe admet une asymptote horizontale d'équation au voisinage de plus l'infini.
On rencontre une forme indéterminée.
On va donc factoriser le numérateur et le dénominateur par .
par quotient
La courbe admet une asymptote horizontale d'équation au voisinage de plus l'infini.
Question 3
Etudier les variations de sur .
Correction
est dérivable sur .
On reconnait la forme avec et .
Ainsi et .
Il en résulte que :
Ainsi .
Or , pour tout réel , on a et .
On peut en conclure que la fonction est croissante sur .
On reconnait la forme avec et .
Ainsi et .
Il en résulte que :
.
Ainsi .
Or , pour tout réel , on a et .
On peut en conclure que la fonction est croissante sur .
Question 4
Déterminer une équation de la tangente à la courbe au point d'abscisse 0.
Correction
On sait que la formule de l'équation de la tangente au point d'abscisse 0 est :
D'une part : alors
D'autre part : alors
Ainsi :
Enfin :
D'une part : alors
D'autre part : alors
Ainsi :
Enfin :
Question 5
Justifier que, pour étudier la position de la courbe par rapport à la tangente , il suffit d'étudier sur le signe de , où .
Correction
Posons une fonction définie sur par .
Cette fonction nous permettra d'étudier la position relative de la courbe par rapport à la tangente .
équivaut successivement à
On va tout mettre au même dénominateur,
Le dénominateur est strictement positif.
Il en résulte que le signe de dépend du numérateur .
Ainsi pour étudier la position de la courbe par rapport à la tangente , il suffit d'étudier sur le signe de , où.
Cette fonction nous permettra d'étudier la position relative de la courbe par rapport à la tangente .
équivaut successivement à
On va tout mettre au même dénominateur,
Le dénominateur est strictement positif.
Il en résulte que le signe de dépend du numérateur .
Ainsi pour étudier la position de la courbe par rapport à la tangente , il suffit d'étudier sur le signe de , où.
Question 6
Calculer et
Correction
est dérivable sur donc :
N'oubliez pas d'utiliser la forme pour dérivée .
On effectue maintenant la dérivée de qui nous donnera .Question 7
Déterminer, en les justifiant, les signes de , et suivant les valeurs de .
Correction
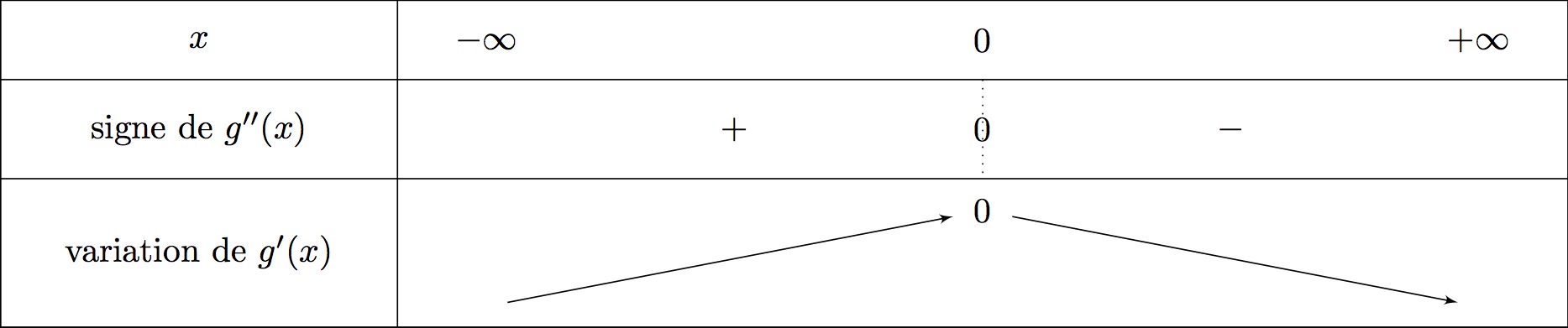
Soit , est du signe de car .
Il en résulte que :
sur et sur .
On en déduit le tableau de variation de .
De plus, on sait que .
.
Ainsi la fonction admet un maximum en qui vaut .
Il en résulte que pour tout réel , .
On en déduit que la fonction est croissante sur .
On résume tout cela dans un tableau de variation :
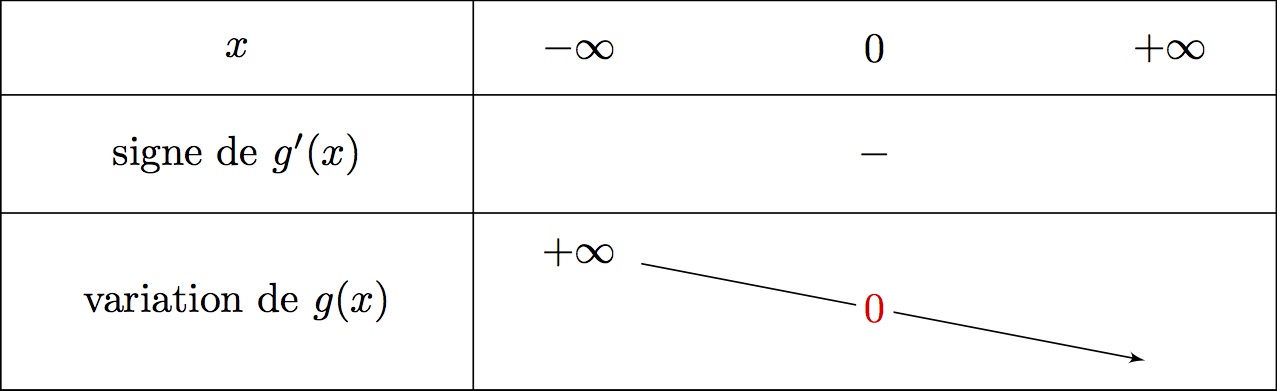 De plus, on sait que :
De plus, on sait que :
On remarque que :
De plus :
Il en résulte que :
sur et sur .
On en déduit le tableau de variation de .

De plus, on sait que .
.
Ainsi la fonction admet un maximum en qui vaut .
Il en résulte que pour tout réel , .
On en déduit que la fonction est croissante sur .
On résume tout cela dans un tableau de variation :

On remarque que :
De plus :
Il en résulte donc que sur et sur .
Question 8
En déduire la position de la tangente par rapport à la courbe .
Correction
D'après la question précédente :
- sur la courbe est au-dessus de la tangente sur
- sur la courbe est en dessous de la tangente sur
Question 9
Partie B
Etude de la suite définie pour tout entier naturel par :
Etude de la suite définie pour tout entier naturel par :
Montrer que
Correction
Une primitive de la forme est
donc
En posant alors .
Ainsi :
Donc une primitive de est .
Ainsi,
Question 10
Montrer que .
En déduire une valeur exacte de .
En déduire une valeur exacte de .
Correction
D'après la question précédente, on sait que .
Ainsi : .
D'où :
Question 11
Montrer que la suite est positive.
Correction
Si sur alors .
On a : qui s'écrit .Pour tout entier naturel et pour tout réel , on a : .
Il en résulte que : alors : .
Question 12
On pose : .
Montrer que pour tout réel , on a :
Correction
Pour tout réel , on a :
équivaut successivement à
équivaut successivement à
Question 13
Etudier le signe de lorsque
Correction
Pour tout réel , on vérifie facilement que .
Le signe de dépend du numérateur .
équivaut successivement à
Il en résulte que : lorsque .
Finalement : lorsque .
Le signe de dépend du numérateur .
équivaut successivement à
Il en résulte que : lorsque .
Finalement : lorsque .
Question 14
En déduire que la suite est décroissante.
Correction
On sait que .
Etudions le signe de .
D'après la question précédente :
Ainsi,
Or lorsque donc . Ainsi .
La suite est décroissante.
Etudions le signe de .
D'après la question précédente :
Ainsi,
Or lorsque donc . Ainsi .
La suite est décroissante.
Question 15
Montrer que, pour tout entier naturel supérieur ou égal à , on a : .
Correction
Pour tout entier naturel supérieur ou égal à , on a :
équivaut successivement à
équivaut successivement à
Question 16
Soit la suite définie pour tout entier supérieur ou égal à par :
Calculer la limite de quand tend vers .
Correction
D'après la question précédente, on sait que
Donc que l'on peut aussi écrire
Ainsi :
par quotient
Donc que l'on peut aussi écrire
Ainsi :
par quotient