La fonction exponentielle
Exercice 2 - Exercice 1
1 min
0
Question 1
Partie A
On considère la fonction définie sur par .
On note la courbe représentative de .
On considère la fonction définie sur par .
On note la courbe représentative de .
Quel est, suivant les valeurs de , le signe de ?
Correction
Par notion de cours, la fonction exponentielle est positive sur . Il en résulte donc que . Le signe de dépend alors uniquement de
- Si .
- Si .
Question 2
Etudier le sens de variation de la fonction .
Correction
Ici on reconnait la forme avec et .
Ainsi et .
Il vient alors que :
.
On factorise par
Pour tout réel , on a .
Il en résulte donc que :
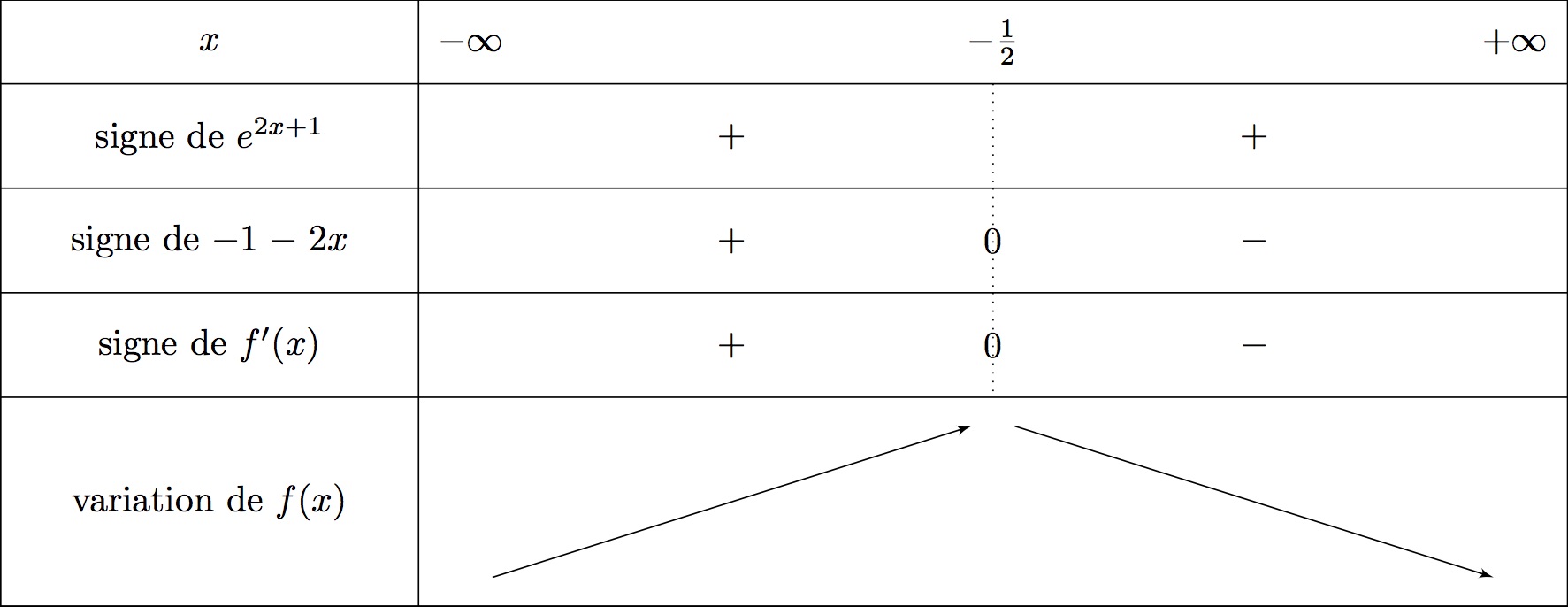
Ainsi et .
Il vient alors que :
.
On factorise par
Pour tout réel , on a .
Il en résulte donc que :
- si alors et donc est croissante sur cet intervalle.
- si alors et donc est décroissante sur cet intervalle.

Question 3
Montrer que
Correction
équivaut successivement à :
Question 4
Etudier les limites de la fonction en , et en .
Correction
Or : ( Formule du cours )
Ainsi .
Il en résulte qu'il existe une asymptote horizontale d'équation .
Question 5
Ecrire une équation de la tangente à au point d'abscisse .
Correction
Question 6
On appelle la représentation graphique dans le repère orthonormé de la fonction définie sur par .
Quel est l'équation de tangente à au point d'abscisse ?
Quel est l'équation de tangente à au point d'abscisse ?
Correction
, la tangente à au point d'abscisse
Question 7
Partie B
On appelle la fonction définie sur par .
On appelle la fonction définie sur par .
Etudier le sens de variation de .
En déduire le signe de suivant les valeurs de .
En déduire le signe de suivant les valeurs de .
Correction
est le produit de fonction dérivable sur , elle est donc dérivable sur cet intervalle.
Ici on reconnait la forme : avec et .
Ainsi et .
Il vient alors que :
est donc du signe .
Il en résulte donc que :
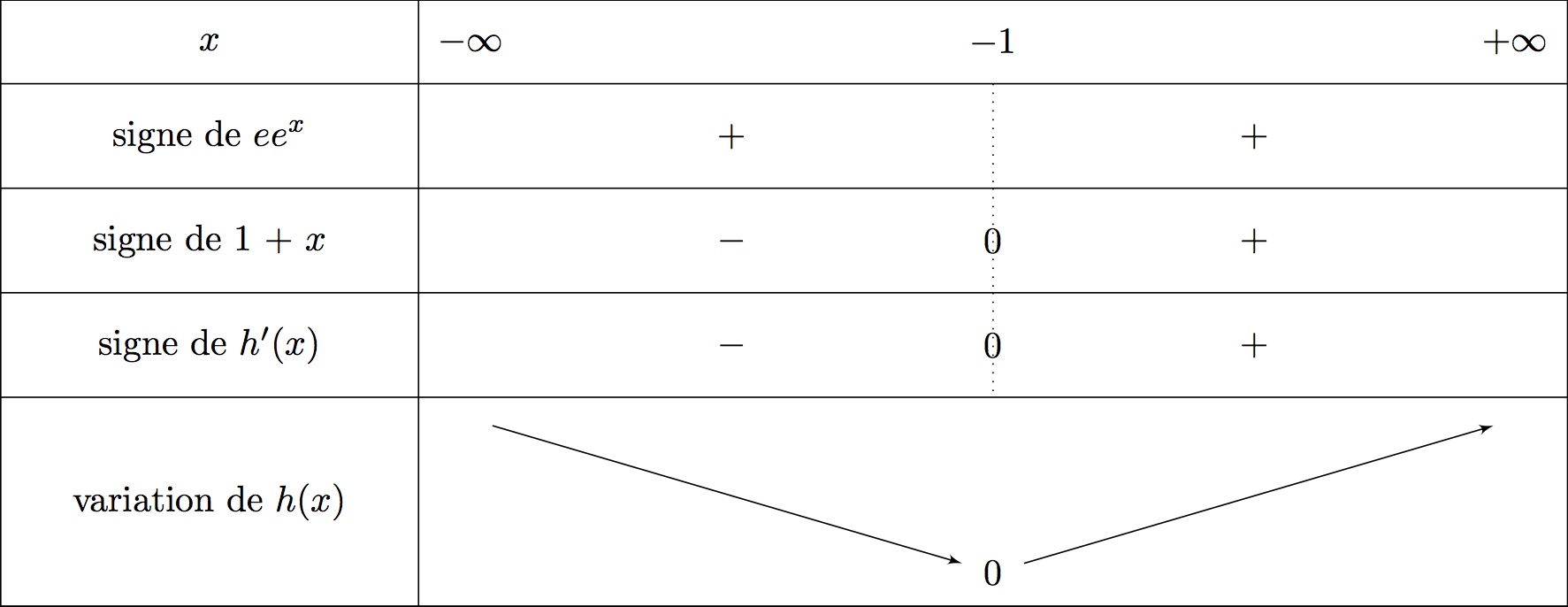 Or c'est-à-dire .
Or c'est-à-dire .
Il en résulte que pour tout réel , la fonction est positive.
Ici on reconnait la forme : avec et .
Ainsi et .
Il vient alors que :
est donc du signe .
Il en résulte donc que :
- si alors et donc est décroissante sur cet intervalle.
- si alors et donc est croissante sur cet intervalle.

Il en résulte que pour tout réel , la fonction est positive.
Question 8
Etudier la position de par rapport à .
Correction
Pour étudier la position des deux courbes, il nous faut étudier le signe de
Or d'où sera du signe de
D'après la question précédente alors
cela signifie que la courbe est au-dessous de la courbe sur .
Or d'où sera du signe de
D'après la question précédente alors
cela signifie que la courbe est au-dessous de la courbe sur .
Question 9
Soit un réel quelconque et le point de la courbe d'abscisse .
Ecrire une équation de tangente à en .
Correction
Une équation de tangente au point est de la forme :
Question 10
La tangente coupe les axes de coordonnées en et .
Calculer, en fonction de , les coordonnées du milieu du segment .
Calculer, en fonction de , les coordonnées du milieu du segment .
Correction
- Si , alors . Donc
- Si , alors . Donc
D'où :
Question 11
Prouver que appartient à .
Correction
appartient à si ces coordonnées vérifient l'équation de
qui est bien l'ordonnée de .
qui est bien l'ordonnée de .