La fonction exponentielle
Exercice 1 - Exercice 1
1 min
0
Pour chacune des propositions suivantes, dire si elle est vraie ou fausse en justifiant la réponse.
Question 1
Soit une fonction définie sur par .
Proposition : « » .
Proposition : « » .
Correction
La proposition est fausse.
est dérivable sur .
On reconnaît la forme : avec et .
Ainsi et .
Il vient alors que :
est dérivable sur .
On reconnaît la forme : avec et .
Ainsi et .
Il vient alors que :
Question 2
Soit une fonction définie sur par .
Proposition : « admet deux asymptotes ».
Proposition : « admet deux asymptotes ».
Correction
La proposition est vraie.
D'une part : calculons :
équivaut successivement à :
car
par quotient : .
Ainsi , il existe une asymptote horizontale d'équation au voisinage de .
D'autre part : calculons :
par quotient :
Ainsi, il existe une asymptote verticale d'équation .
D'une part : calculons :
équivaut successivement à :
car
par quotient : .
Ainsi , il existe une asymptote horizontale d'équation au voisinage de .
D'autre part : calculons :
par quotient :
Ainsi, il existe une asymptote verticale d'équation .
Question 3
Soit une fonction définie sur par
Soit le point d'abscisse : .
Proposition : « la tangente à la courbe au point d'abscisse est ».
Soit le point d'abscisse : .
Proposition : « la tangente à la courbe au point d'abscisse est ».
Correction
La proposition est fausse.
On commence par calculer la dérivée de .
est dérivable sur et .
L'équation de la tangente à la courbe au point d'abscisse s'écrit :
Calculons
Calculons
Or : donc ,
On commence par calculer la dérivée de .
est dérivable sur et .
L'équation de la tangente à la courbe au point d'abscisse s'écrit :
Or : donc ,
Question 4
Soit une fonction définie sur par où et sont deux réels.
La courbe représentative de la fonction passe par le point et admet en ce point une tangente parallèle à la droite d'équation .
Proposition : « la fonction s'écrit ».
La courbe représentative de la fonction passe par le point et admet en ce point une tangente parallèle à la droite d'équation .
Proposition : « la fonction s'écrit ».
Correction
La proposition est vraie.
D'après l'énoncé, on en déduit deux informations
Ensuite, calculons la dérivée de .
est dérivable sur , on reconnaît la forme avec et .
Ainsi et .
D'où :
Or : , il s'ensuit que :
(rappel )
Finalement :
D'après l'énoncé, on en déduit deux informations
- Le nombre désigne le coefficient directeur de la droite tangente à la courbe au point d'abscisse . Dans cet exercice la tangente au point d'abscisse 0 est parallèle à la droite d'équation donc .
Ensuite, calculons la dérivée de .
est dérivable sur , on reconnaît la forme avec et .
Ainsi et .
D'où :
Or : , il s'ensuit que :
(rappel )
Finalement :
Question 5
Soit :
Proposition : « » .
Proposition : « » .
Correction
La proposition est fausse.
équivaut successivement à :
équivaut successivement à :
Question 6
Soit une fonction définie sur par .
Proposition : « ».
Proposition : « ».
Correction
La proposition est vraie.
équivaut successivement à :
(on a multiplié le numérateur et le dénominateur par )
équivaut successivement à :
(on a multiplié le numérateur et le dénominateur par )
Question 7
Soit une fonction définie par .
Proposition : « Le domaine de définition de est : » .
Proposition : « Le domaine de définition de est : » .
Correction
La proposition est vraie.
une fonction définie si et seulement si
équivaut successivement à
car
Finalement le domaine de définition de est
une fonction définie si et seulement si
équivaut successivement à
car
Finalement le domaine de définition de est
Question 8
Soit une fonction définie sur par
Proposition : « » .
Proposition : « » .
Correction
La proposition est fausse.
est dérivable sur
On reconnaît la forme : avec et
Ainsi et .
Ainsi :
On dérive maintenant afin d'obtenir .
On reconnait la forme avec et
Ainsi et .
Ainsi :
Maintenant calculons :
équivaut à :
est dérivable sur
On reconnaît la forme : avec et
Ainsi et .
Ainsi :
On dérive maintenant afin d'obtenir .
On reconnait la forme avec et
Ainsi et .
Ainsi :
Maintenant calculons :
équivaut à :
Question 9
Soit une fonction définie sur par .
Proposition : « » .
Proposition : « » .
Correction
La proposition est fausse.
Ainsi :
D'où :
La vraie réponse est :
Une primitive de la forme est de la forme
Soient donc Ainsi :
D'où :
La vraie réponse est :
Question 10
Soit une fonction définie sur par .
Proposition : « est croissante sur » .
Proposition : « est croissante sur » .
Correction
La proposition est vraie.
Etudions le signe de la dérivée de .
est dérivable sur.
Posons tout d'abord et calculons la dérivée de .
On reconnaît la forme : avec et .
Ainsi et .
Maintenant nous pouvons calculer la dérivée de où avec
D'après le cours : .
Nous avons calculé précédemment .
Il vient alors que :
Donc :
Soit , on sait que : et .
Donc le signe de dépend de .
Comme alors :
équivaut successivement à :
Il en résulte donc que donc que la fonction est croissante sur .
Etudions le signe de la dérivée de .
est dérivable sur.
Posons tout d'abord et calculons la dérivée de .
On reconnaît la forme : avec et .
Ainsi et .
Maintenant nous pouvons calculer la dérivée de où avec
D'après le cours : .
Nous avons calculé précédemment .
Il vient alors que :
Donc :
Soit , on sait que : et .
Donc le signe de dépend de .
Comme alors :
équivaut successivement à :
Il en résulte donc que donc que la fonction est croissante sur .
Question 11
Soit une fonction définie sur par .
Proposition : « admet un minimum qui vaut ».
Proposition : « admet un minimum qui vaut ».
Correction
La proposition est fausse.
Etudions le signe de la dérivée de .
est dérivable sur .
Posons tout d'abord et calculons la dérivée de .
On reconnaît la forme = avec et .
Ainsi et .
Maintenant nous pouvons calculer la dérivée de , il vient alors que :
Nous avons mis tout au même dénominateur.
Soit , on sait que .
Donc le signe de dépend de .
Pour étudier le signe de , on va commencer par effectuer le changement de variable .
Ainsi s'écrit .
On reconnaît un trinôme du second degré. On utilise le discriminant.
Les racines sont alors et .
On peut donc factoriser ainsi :
Autrement dit :
Il nous suffit donc d'étudier le signe de à l'aide d'un tableau de signe qui nous donnera le signe de .
D'une part : équivaut à :
or et comme alors pour tout réel
D'autre part : équivaut à :
Dressons enfin le tableau de variation de :
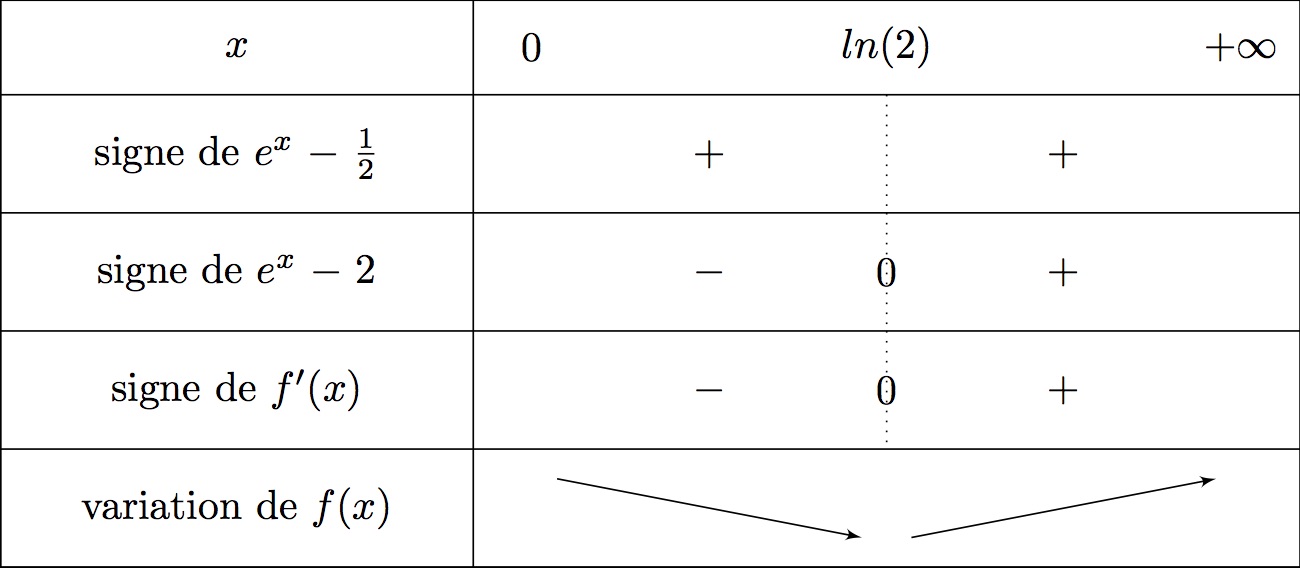
admet donc un minimum lorsque .
Ainsi :
admet un minimum qui vaut .
Etudions le signe de la dérivée de .
est dérivable sur .
Posons tout d'abord et calculons la dérivée de .
On reconnaît la forme = avec et .
Ainsi et .
Maintenant nous pouvons calculer la dérivée de , il vient alors que :
Nous avons mis tout au même dénominateur.
Soit , on sait que .
Donc le signe de dépend de .
Pour étudier le signe de , on va commencer par effectuer le changement de variable .
Ainsi s'écrit .
On reconnaît un trinôme du second degré. On utilise le discriminant.
Les racines sont alors et .
On peut donc factoriser ainsi :
Si alors : vu en 1ère S
Autrement dit :
Il nous suffit donc d'étudier le signe de à l'aide d'un tableau de signe qui nous donnera le signe de .
D'une part : équivaut à :
or et comme alors pour tout réel
D'autre part : équivaut à :
Dressons enfin le tableau de variation de :

admet donc un minimum lorsque .
Ainsi :
admet un minimum qui vaut .
Question 12
Soit une fonction définie sur par .
Proposition : « et » .
Proposition : « et » .
Correction
La proposition est fausse.
Ici il s'agit de limite par composition.
Commençons par calculer
Dans un premier temps .
On pose
D'où : .
Finalement, par composition
Ensuite, calculons
Dans un premier temps :
par quotient .
On pose
D'où : .
Finalement, par composition :
Ici il s'agit de limite par composition.
Commençons par calculer
Dans un premier temps .
On pose
D'où : .
Finalement, par composition
Ensuite, calculons
Dans un premier temps :
par quotient .
On pose
D'où : .
Finalement, par composition :
Question 13
Soit une fonction définie sur par .
Proposition : « et » .
Proposition : « et » .
Correction
La proposition est vraie.
On sait que : .
Nous allons multiplier le numérateur et le dénominateur par .
équivaut à :
Passons maintenant à la limite :
par quotient
On sait que : .
Nous allons multiplier le numérateur et le dénominateur par .
équivaut à :
Passons maintenant à la limite :
par quotient
.
Question 14
Correction
La proposition est vraie.
Nous allons commencer par calculer la limite du numérateur .
Ici, il s'agit d'une limite par composition.
On commence par calculer .
On pose .
Ainsi : .
Par composition :
par quotient, on rencontre ici une forme indéterminée.
Ici, pour pouvoir calculer la limite, nous allons faire apparaitre un produit.
. Il en résulte donc que :
Finalement :
Nous allons commencer par calculer la limite du numérateur .
Ici, il s'agit d'une limite par composition.
On commence par calculer .
On pose .
Ainsi : .
Par composition :
par quotient, on rencontre ici une forme indéterminée.
Ici, pour pouvoir calculer la limite, nous allons faire apparaitre un produit.
. Il en résulte donc que :
Finalement :
Question 15
A l'aide de la représentation graphique ci-dessous de la fonction :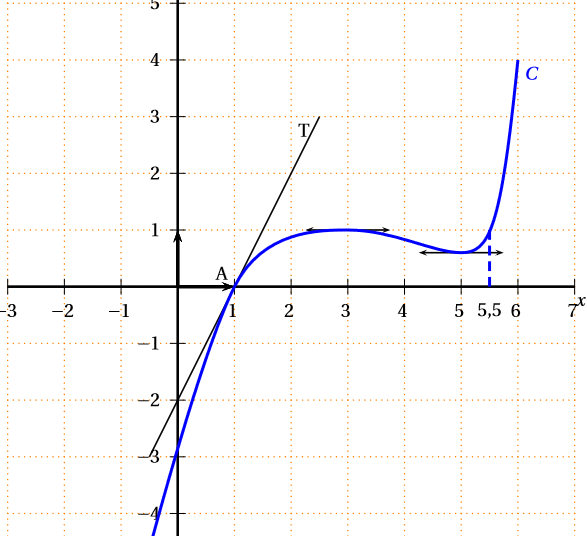 On a :
On a :

Correction
La proposition est fausse.
correspond au coefficient directeur de la tangente à la courbe au point d'abscisse . Les points et appartiennent à cette tangente.
Les points et appartiennent à cette tangente.
A l'aide du point et du point on va pouvoir donner le coefficient directeur de la tangente.
Ainsi :
correspond au coefficient directeur de la tangente à la courbe au point d'abscisse .

A l'aide du point et du point on va pouvoir donner le coefficient directeur de la tangente.
Ainsi :