Estimation et intervalles
Exercices types : ème< partie - Exercice 1
30 min
50
Les parties , et peuvent être traitées indépendamment.
Partie A .
Partie A .
Question 1
Une société de location de voitures s'intéresse à l’état mécanique de son parc automobile afin d’anticiper les frais d’entretien. On dispose des données suivantes :
des voitures sont sous garantie ; pour des voitures sous garantie, une réparation est nécessaire ; pour de celles qui ne sont plus sous garantie, une réparation est nécessaire. On choisit une voiture au hasard dans le parc et on considère les évènements suivants :
• : « la voiture est sous garantie » ;
• : « une réparation est nécessaire ».
• : « la voiture est sous garantie » ;
• : « une réparation est nécessaire ».
Traduire la situation par un arbre pondéré.
Correction
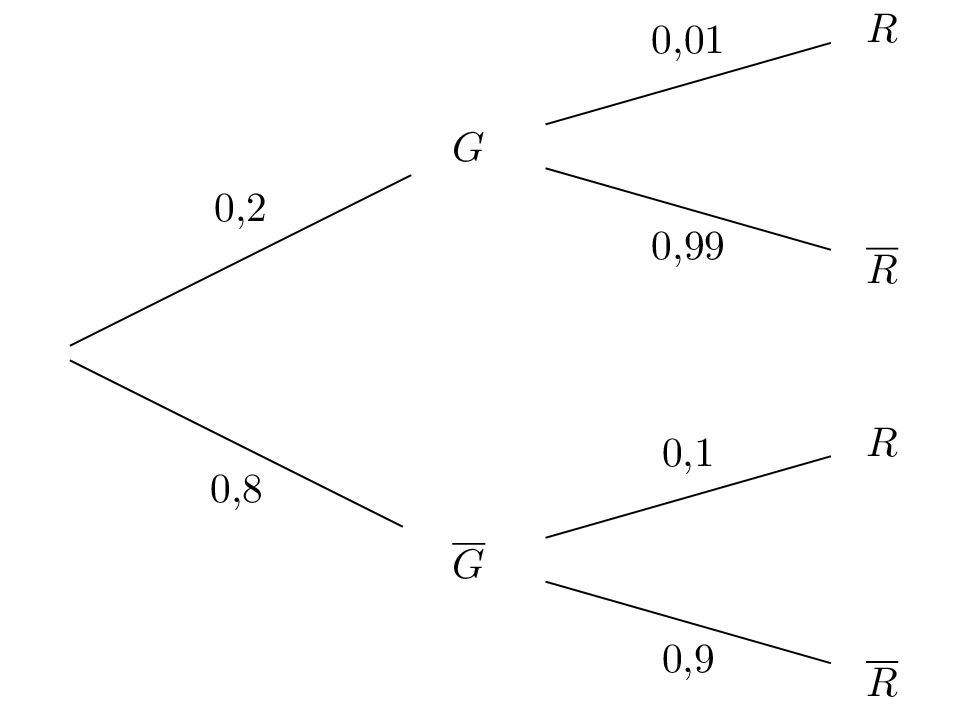
Question 2
Calculer la probabilité que la voiture choisie soit sous garantie et nécessite une réparation.
Correction

Question 3
Justifier que .
Correction

D'après la formule des probabilités totales on a :
Soit :
Ainsi :
Question 4
Il s'avère que la voiture choisie nécessite une réparation. Quelle est la probabilité qu’elle soit sous garantie? On arrondira le résultat à .
Correction

d'où :
Question 5
La société de location fait appel à un garage pour l’entretien de son parc automobile. L’entretien consiste en une révision à laquelle s’ajoutent d’éventuelles réparations. Les conditions commerciales du garage sont les suivantes :
si la voiture est encore sous garantie, l’entretien est gratuit ; si la voiture n’est plus sous garantie, l’entretien est facturé de la manière suivante : la révision coûte euros et, si une réparation est nécessaire, il faut rajouter euros.
Sachant que son parc automobile compte voitures, est-il raisonnable pour la société de location de prévoir un budget annuel de euros pour l’entretien de l’ensemble des voitures?
On pourra introduire la variable aléatoire qui représente le coût d’entretien d’une voiture.
On pourra introduire la variable aléatoire qui représente le coût d’entretien d’une voiture.
Correction

On va calculer le coût moyen par voiture qui correspond à l’espérance mathématique de . Il y a trois cas de figures :
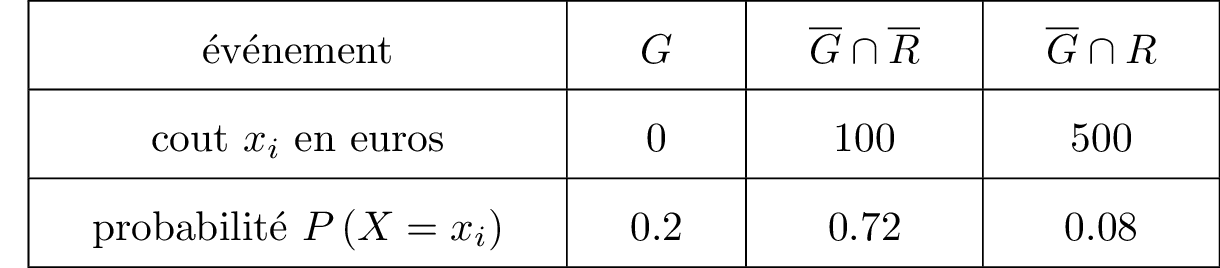
- On appelle l’espérance mathématique de la variable , la quantité notée définie par :
Soit
Chaque voiture coûte en moyenne euros .
il y a voitures, ce qui fait une dépense totale de euros .
Le budget de euros est alors insuffisant.
Question 6
Partie B .
La société de location propose à ses clients deux contrats de location : un contrat de courte durée (inférieure à jours) et un contrat de longue durée (de à jours). La directrice de cette société affirme que des clients demandent un contrat de courte durée. Sur les derniers contrats signés l’année précédente, étaient des contrats de courte durée.
La société de location propose à ses clients deux contrats de location : un contrat de courte durée (inférieure à jours) et un contrat de longue durée (de à jours). La directrice de cette société affirme que des clients demandent un contrat de courte durée. Sur les derniers contrats signés l’année précédente, étaient des contrats de courte durée.
En supposant que l’affirmation de la directrice est correcte, déterminer un intervalle de fluctuation asymptotique au seuil de de la fréquence des contrats de courte durée.
Correction
Il faut vérifier les conditions suivantes , et avec et .
On a alors :
Ici est une valeur approchée par défaut de
Ici est une valeur approchée par excès de
- donc
- donc
- donc
On a alors :
Ici est une valeur approchée par défaut de
Ici est une valeur approchée par excès de
Question 7
Que peut-on penser de l’affirmation de la directrice?
Correction
Sur les derniers contrats signés l’année précédente, étaient des contrats de courte durée.
On détermine la fréquence des contrats de courte durée dans l'échantillon, il vient alors que :
Or , donc la fréquence des contrats de courte durée n'est pas dans l'intervalle. Donc, au risque de , l’affirmation de la directrice n’est pas correcte.
On détermine la fréquence des contrats de courte durée dans l'échantillon, il vient alors que :
Or , donc la fréquence des contrats de courte durée n'est pas dans l'intervalle. Donc, au risque de , l’affirmation de la directrice n’est pas correcte.
Question 8
Partie C .
On modélise le nombre de kilomètres parcourus par les clients louant une voiture pour une semaine par une variable aléatoire suivant la loi normale d’espérance et d’écart-type .
On modélise le nombre de kilomètres parcourus par les clients louant une voiture pour une semaine par une variable aléatoire suivant la loi normale d’espérance et d’écart-type .
Quelle est la probabilité que le client louant la voiture pour une semaine roule entre km et km? On arrondira le résultat à .
Correction
Nous devons calculer
Avec une calculatrice Texas, pour on tape NormalFrep(valeur min, valeur max, espérance, écart type)
C'est-à-dire ici NormalFrep( , , , ) puis on tape sur Enter et on obtient :
Avec une calculatrice Casio Graph 35+, pour on tape :
Puis on tape sur EXE et on obtient :
Avec une calculatrice Texas, pour on tape NormalFrep(valeur min, valeur max, espérance, écart type)
C'est-à-dire ici NormalFrep( , , , ) puis on tape sur Enter et on obtient :
Avec une calculatrice Casio Graph 35+, pour on tape :
Normal C.D
Lower : valeur Minimale
Upper : valeur Maximale
: écart type
: espérance
Lower : valeur Minimale
Upper : valeur Maximale
: écart type
: espérance
Puis on tape sur EXE et on obtient :
Question 9
La société de location souhaite faire une offre promotionnelle aux de ses clients parcourant le moins de kilomètres en une semaine. En-dessous de quel kilométrage hebdomadaire, arrondi à l’unité, un client sera-t-il concerné par cette offre?
Correction
Nous devons calculer
Avec une calculatrice Texas, pour on tape InvNorm(valeur donnée, espérance, écart type)
C'est-à-dire ici InvNorm( , , ) puis on tape sur Enter et on obtient :
Avec une calculatrice Casio Graph 35+, pour on tape :
puis on tape sur EXE et on obtient :
En-dessous de km hebdomadaire, un client sera alors concerné par l'offre promotionnelle.
Avec une calculatrice Texas, pour on tape InvNorm(valeur donnée, espérance, écart type)
C'est-à-dire ici InvNorm( , , ) puis on tape sur Enter et on obtient :
Avec une calculatrice Casio Graph 35+, pour on tape :
Normal inverse
Data : Variable
Tail : Left car c'est
Area :
: Ecart type
: Espérance
Data : Variable
Tail : Left car c'est
Area :
: Ecart type
: Espérance
puis on tape sur EXE et on obtient :
En-dessous de km hebdomadaire, un client sera alors concerné par l'offre promotionnelle.