Exercice 2 - Exercice 1

La bonne réponse est a.
On note $$A$$ l'évènement « être une femme ».
On note $$B$$ l'évènement « faire de la compétition ».
On va établir l'arbre de probabilité relatif à l'énoncé.
On obtient alors :
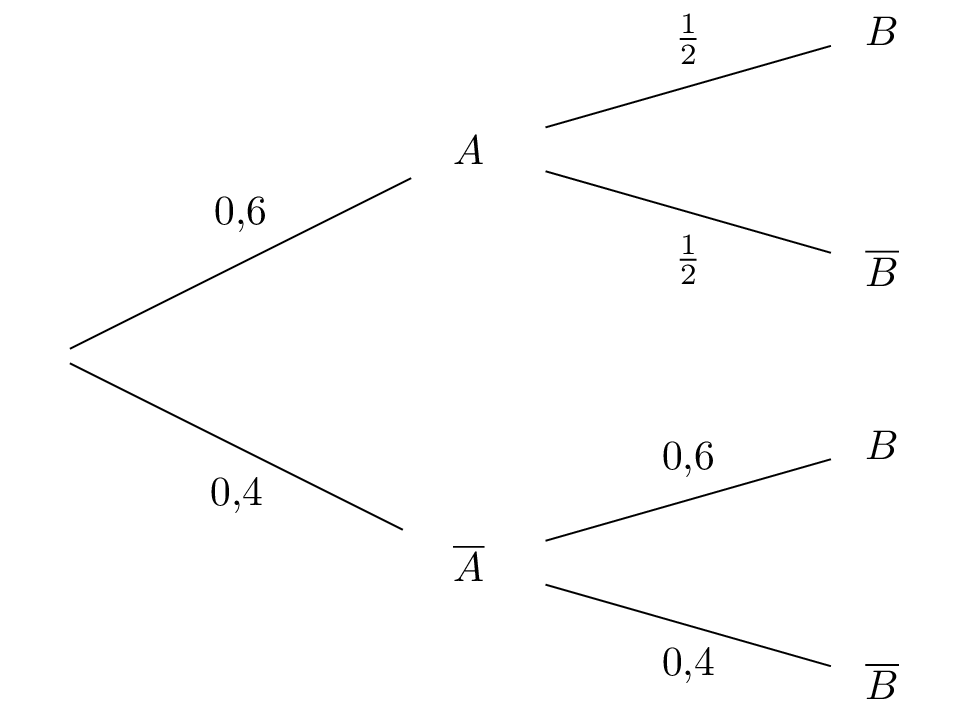On interroge une personne au hasard : cette personne fait de la compétition. Quelle est la probabilité que ce soit une femme ?
Il s'agit d'ici d'une probabilité conditionnelle.
On sait que la personne fait de la compétition, et on veut que cela soit une femme.
Il s'agit donc de $$P_{B} \left(A\right)=\frac{P\left(A\cap B\right)}{P\left(B\right)}$$.
On va calculer $$P\left(A\cap B\right)$$ et on calculer $$P\left(B\right)$$.
D'une part, on calcule $$P\left(A\cap B\right)$$
$$P\left(A\cap B\right)=P\left(A\right)\times P_{A} \left(B\right)$$
$$P\left(A\cap B\right)=0,6\times \frac{1}{2} =0,3$$
D'autre part, on calcule $$P\left(B\right)$$
$$A$$ et $$\overline{A}$$ forment une partition de l'univers.
D'après la formule des probabilités totales on a :
$$P\left(B\right)=P\left(A\cap B\right)+P\left(\overline{A}\cap B\right)$$
$$P\left(B\right)=P\left(A\right)\times P_{A} \left(B\right)+P\left(\overline{A}\right)\times P_{\overline{A}} \left(B\right)$$
Soit : $$P\left(B\right)=0,6\times \frac{1}{2} +0,4\times 0,6$$
Ainsi :
Enfin : $$P_{B} \left(A\right)=\frac{P\left(A\cap B\right)}{P\left(B\right)}$$ s'écrit

La bonne réponse est c.
Rédaction type pour la loi binomiale.

On doit calculer $$P\left(X\ge 1\right)$$. Or $$P\left(X\ge 1\right)=1-P\left(X=0\right)$$
Pour le calcul de $$P\left(X=0\right)$$
Avec une Texas , on tape pour $$P\left(X=0\right)$$ (cf. fiche Utiliser la loi binomiale avec une Texas)
2$${}^{nd}$$ - DISTR -- puis choisir
BinomFdp(valeur de n, valeur de p, valeur de k ) c'est-à-dire ici BinomFdp($$4$$ , $$0$$ , $$4$$ , $$0$$) puis taper sur enter et vous obtiendrez arrondi à $$10^{-3}$$près.
Pour certaine version de Texas, on aura BinomPdf au lieu de BinomFdp.
Enfin $$P\left(X\ge 1\right)=1-P\left(X=0\right)$$ soit $$P\left(X\ge 1\right)=1-P\left(X=0\right)$$ d'où

Avec une Casio Graph 35+ ou modèle supérieur, on tape pour $$P\left(X=0\right)$$ (cf fiche Utiliser la loi binomiale avec une Casio)
Choisir Menu Stat puis DIST puis BINM et prendre BPD puis VAR. On remplit le tableau de la manière qui suit

puis taper sur EXE et vous obtiendrez $$<$$ arrondi à $$10^{-3}$$ près.
Enfin $$P\left(X\ge 1\right)=1-P\left(X=0\right)$$ soit $$P\left(X\ge 1\right)=1-P\left(X=0\right)$$ d'où

La bonne réponse est a.
On sait que $$P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)-P\left(A\cap B\right)$$
De plus, $$A$$ et $$B$$ sont deux évènements indépendants.
Il vient alors que : $$P\left(A\cap B\right)=P\left(A\right)\times P\left(B\right)$$
$$P\left(A\cap B\right)=\frac{1}{3} \times \frac{1}{4} =\frac{1}{12}$$
Finalement,
$$P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)-P\left(A\cap B\right)$$
$$P\left(A\cup B\right)=\frac{1}{3} +\frac{1}{4} -\frac{1}{12}$$

La bonne réponse est b.

La bonne réponse est c.

La bonne réponse est a.
Le jeu est équitable si et seulement si l'espérance est nulle.
Il vient alors que :
$$-2\times \frac{5}{12} +0\times \frac{1}{3} +1\times \frac{1}{6} +5\times m=0$$
$$-\frac{10}{12} +\frac{1}{6} +5\times m=0$$
$$-\frac{10}{12} +\frac{2}{12} +5\times m=0$$
$$-\frac{8}{12} +5\times m=0$$
$$-\frac{8}{12} +5\times m=0$$
$$-\frac{2}{3} +5\times m=0$$
$$5\times m=\frac{2}{3}$$
$$m=\frac{2}{3} \times \frac{1}{5}$$

La bonne réponse est b.
Ainsi :
$$E\left(X\right)=1,8$$ donc
$$\sigma \left(X\right)=1,2$$ d'où :
Comme : $$n\times p=1,8$$ et $$\sqrt{n\times p\times \left(1-p\right)}=1,2$$. Il vient alors que :
$$\sqrt{1,8\times \left(1-p\right)} =1,2$$
$$1,8\times \left(1-p\right)=1,2^{2}$$
$$1,8\times \left(1-p\right)=1,44$$
$$1-p=\frac{1,44}{1,8}$$
$$1-p=0,8$$
$$-p=0,8-1$$
$$-p=-0,2$$
Ainsi :
Or : $$n\times p=1,8$$ , il vient alors que :
$$n\times 0,2=1,8$$
$$n=\frac{1,8}{0,2}$$
D'où :