Les suites numériques
Exercice 7 - Exercice 1
1 min
0
Une école de danse a ouvert ses portes en . Cette année là, elle comptait inscrits. Chaque année, elle prévoit une augmentation de des inscriptions ainsi que désinscriptions. Pour tout entier naturel , on note le nombre d’inscrits l’année . Chaque inscrit paye une cotisation annuelle de euros, sur laquelle l’école conserve un bénéfice de euros après avoir payé tous ses frais fixes. L’école économise ce bénéfice afin de construire une nouvelle salle de danse. Pour cela, elle a besoin d’un budget de euros.
Question 1
Partie A .
Les données sont saisies dans une feuille de calcul donnée ci-dessous. Le format de cellule a été choisi pour que les nombres de la colonne soient arrondis à l’unité.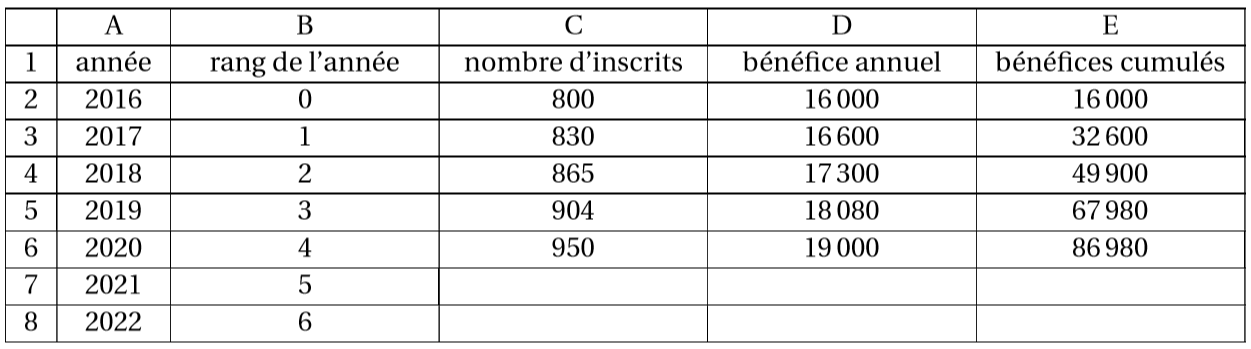
Les données sont saisies dans une feuille de calcul donnée ci-dessous. Le format de cellule a été choisi pour que les nombres de la colonne soient arrondis à l’unité.

Quelle formule peut-on saisir en pour obtenir, par recopie vers le bas, le nombre d’inscrits l’année de rang ?
Correction
La formule que l’on saisit en pour obtenir, par recopie vers le bas, le nombre d’inscrits l’année de rang est
Question 2
Quelle formule peut-on saisir en pour obtenir, par recopie vers le bas, le bénéfice cumulé à l’année de rang ?
Correction
La formule que l’on saisit en pour obtenir, par recopie vers le bas, le bénéfice cumulé à l’année de rang est
Question 3
Compléter sur le tableau initial, les six cellules des lignes qui correspondent aux années et .
Correction
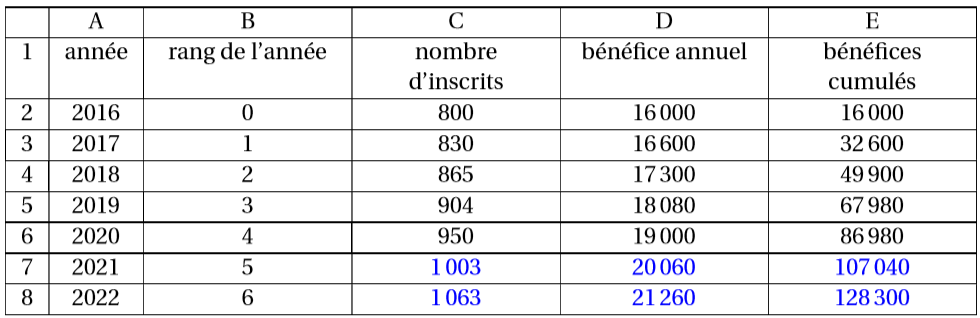
Question 4
En quelle année l’école pourra-t-elle construire sa nouvelle salle de danse?
Correction
L’école dépassera euros comme bénéfices cumulés en , c’est donc en qu’elle pourra construire sa nouvelle salle de danse.
Question 5
Partie B .
Justifier que, pour tout entier naturel , et préciser le premier terme .
Correction
Soit le nombre d’inscrits l’année et le nombre d’inscrits l’année suivante.
On passe du nombre d’inscrits l’année au nombre d’inscrits l’année en ajoutant , donc on multiplie par le coefficient multiplicateur . On constate ensuite désinscriptions c'est à dire on retranche . Il en résulte donc que .
Le nombre d’inscrits en est donc .
Le nombre d’inscrits en est donc .
Question 6
On considère la suite définie, pour tout entier naturel , par .
Montrer que la suite est une suite géométrique. Préciser sa raison et son premier terme .
Correction
On va écrire maintenant l'expression au rang , il vient alors que :
On connait l'expression de , on la remplace et on obtient :
Or : donc :
Ainsi la suite est géométrique de raison et de premier terme donc
Question 7
Pour tout entier naturel , exprimer en fonction de .
Correction
- L'expression de en fonction de est donnée par la formule
Question 8
En déduire que pour tout entier naturel n, .
Correction
On sait que : donc :
Il vient alors que :
Il vient alors que :
Question 9
À partir de quelle année, cette école accueillera-t-elle plus de adhérents?
Correction
Cette école accueillera plus de adhérents pour la première valeur de telle que . Il en résulte donc :
équivaut successivement à :
Or :
Il en résulte donc que c’est à partir de donc de que le nombre d’élèves de cette école dépassera les .
équivaut successivement à :
Or :
Il en résulte donc que c’est à partir de donc de que le nombre d’élèves de cette école dépassera les .