Les lois continues
Exercice 4 - Exercice 1
1 min
0
Un fabricant produit des pneus de deux catégories, la catégorie « pneu neige » et la catégorie « pneu classique ».
Sur chacun d'eux, on effectue des tests de qualité pour améliorer la sécurité.
On dispose des informations suivantes sur le stock de production :
Un client choisit un pneu au hasard dans le stock de production. On note :
Dans tout cet exercice, les résultats seront arrondis au millième.
Sur chacun d'eux, on effectue des tests de qualité pour améliorer la sécurité.
On dispose des informations suivantes sur le stock de production :
- Le stock contient de pneus neige ;
- Parmi les pneus neige, ont réussi les tests de qualité ;
- Parmi les pneus classiques, ont réussi les tests de qualité.
Un client choisit un pneu au hasard dans le stock de production. On note :
- L'évènement : « Le pneu choisi est un pneu neige « ;
- L'évènement : « Le pneu choisi est un pneu classique » ;
- L'évènement : « Le pneu choisi a réussi les tests de qualité »
Dans tout cet exercice, les résultats seront arrondis au millième.
Question 1
Partie A
Illustrer la situation à l'aide d'un arbre pondéré.
Correction
D'après l'énoncé, on en déduit l'arbre suivant.
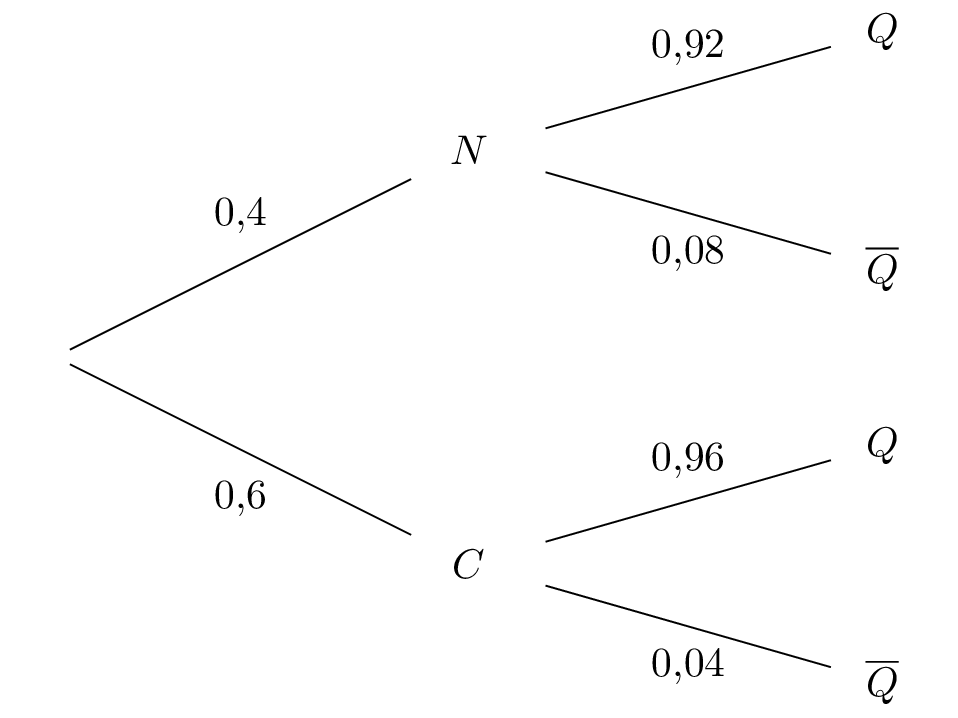

Question 2
Calculer la probabilité de l'évènement et interpréter ce résultat par une phrase.
Correction
En prenant un pneu au hasard dans le stock, la probabilité de choisir un pneu neige qui a réussi les tests de qualité est de .
Question 3
Montrer que .
Correction
Les évènements et forment une partition de l'univers.
D'après la formule des probabilités totales on a :
D'après la formule des probabilités totales on a :
Question 4
Sachant que le pneu choisi a réussi les tests de qualité, quelle est la probabilité que ce pneu soit un pneu neige ?
Correction
On cherche .
Or,
Sachant que le pneu choisi a réussi les tests de qualité, la probabilité que ce pneu soit un pneu neige est environ de .
Or,
Sachant que le pneu choisi a réussi les tests de qualité, la probabilité que ce pneu soit un pneu neige est environ de .
Question 5
Partie B
On appelle durée de vie d'un pneu la distance parcourue avant d'atteindre le témoin d'usure.
On note la variable aléatoire qui associe à chaque pneu classique sa durée de vie, exprimée en milliers de kilomètres.
On admet que la variable aléatoire suit la loi normale d'espérance et d'écart-type .
On appelle durée de vie d'un pneu la distance parcourue avant d'atteindre le témoin d'usure.
On note la variable aléatoire qui associe à chaque pneu classique sa durée de vie, exprimée en milliers de kilomètres.
On admet que la variable aléatoire suit la loi normale d'espérance et d'écart-type .
Quelle est la probabilité qu'un pneu classique ait une durée de vie inférieure à 25 milliers de kilomètres ?
Correction
On souhaite calculer .
Première méthode :
On sait que .
En déterminant avec la calculatrice, cela donne :
Deuxième méthode :
Il faut calculer ici
Pour le calcul de
Avec une Texas, on tape pour NormalFrep(valeur min,valeur max ,espérance , écart type ) c'est-à-dire ici NormalFrep( , , , ) puis taper sur enter et vous obtiendrez :
Avec une Casio Graph 35+, on tape pour :
Puis taper sur EXE et vous obtiendrez
Première méthode :
On sait que .
En déterminant avec la calculatrice, cela donne :
Deuxième méthode :
Il faut calculer ici
Pour le calcul de
Avec une Texas, on tape pour NormalFrep(valeur min,valeur max ,espérance , écart type ) c'est-à-dire ici NormalFrep( , , , ) puis taper sur enter et vous obtiendrez :
Avec une Casio Graph 35+, on tape pour :
Normal C.D
Lower : Valeur Minimale
Upper : Valeur Maximale
: Ecart type
: Espérance
Lower : Valeur Minimale
Upper : Valeur Maximale
: Ecart type
: Espérance
Puis taper sur EXE et vous obtiendrez
Question 6
Déterminer la valeur du nombre pour que, en probabilité, 20% des pneus classiques aient une durée de vie supérieure à kilomètres.
Correction
On cherche le réel vérifiant .
Or, , donc , équivaut à .
Pour le calcul de :
Avec une Texas, on tape pour InvNorm(valeur donné , espérance , écart type ) c'est-à-dire ici InvNorm( , , ) puis taper sur enter et vous obtiendrez :
Pas besoin d'indiquer l'espérance et l'écart type car il s'agit de la loi normale centrée réduite
Avec une Casio Graph 35+, on tape pour
Puis taper sur EXE et vous obtiendrez
Or, , donc , équivaut à .
Pour le calcul de :
Avec une Texas, on tape pour InvNorm(valeur donné , espérance , écart type ) c'est-à-dire ici InvNorm( , , ) puis taper sur enter et vous obtiendrez :
Pas besoin d'indiquer l'espérance et l'écart type car il s'agit de la loi normale centrée réduite
Avec une Casio Graph 35+, on tape pour
Normal inverse
Data : Variable
Tail : Left car c'est
Area :
: Ecart type
: Espérance
Data : Variable
Tail : Left car c'est
Area :
: Ecart type
: Espérance
Puis taper sur EXE et vous obtiendrez
Question 7
Partie C
Une enquête de satisfaction effectuée l'an dernier a révélé que des clients étaient satisfaits de la tenue de route des pneus du fabricant.
Ce dernier souhaite vérifier si le niveau de satisfaction a été le même cette année.
Pour cela, il décide d'interroger un échantillon de clients afin de conclure sur l'hypothèse d'un niveau de satisfaction maintenu.
Parmi les clients interrogés, sont satisfaits de la tenue de route.
Une enquête de satisfaction effectuée l'an dernier a révélé que des clients étaient satisfaits de la tenue de route des pneus du fabricant.
Ce dernier souhaite vérifier si le niveau de satisfaction a été le même cette année.
Pour cela, il décide d'interroger un échantillon de clients afin de conclure sur l'hypothèse d'un niveau de satisfaction maintenu.
Parmi les clients interrogés, sont satisfaits de la tenue de route.
Quelle va être la conclusion du directeur avec un niveau de confiance ?
Détailler les calculs, la démarche et l'argumentation.
Détailler les calculs, la démarche et l'argumentation.
Correction
Posons et .
Alors , et .
Les conditions sont respectées, on peut donc déterminer l'intervalle de fluctuation asymptotique.
Supposons que le taux de satisfaction reste le même que celui de l'année précédente.
En choisissant un échantillon aléatoire de 900 personnes parmi les clients, on a donc une probabilité de 95% d'avoir une fréquence, sur l'échantillon, de clients satisfaits appartenant à l'intervalle
Or, (arrondi par défaut) et (arrondi par excès).
Sous l'hypothèse d'un taux de satisfaction maintenu, on obtient comme intervalle de fluctuation asymptotique pour la fréquence ce clients satisfaits sur un échantillon de 900 personnes l'intervalle .
Sur l'échantillon, la fréquence observée de clients satisfaits est .
On rejette donc, au seuil de , l'hypothèse d'un taux de satisfaction maintenu.
Alors , et .
Les conditions sont respectées, on peut donc déterminer l'intervalle de fluctuation asymptotique.
Supposons que le taux de satisfaction reste le même que celui de l'année précédente.
En choisissant un échantillon aléatoire de 900 personnes parmi les clients, on a donc une probabilité de 95% d'avoir une fréquence, sur l'échantillon, de clients satisfaits appartenant à l'intervalle
Or, (arrondi par défaut) et (arrondi par excès).
Sous l'hypothèse d'un taux de satisfaction maintenu, on obtient comme intervalle de fluctuation asymptotique pour la fréquence ce clients satisfaits sur un échantillon de 900 personnes l'intervalle .
Sur l'échantillon, la fréquence observée de clients satisfaits est .
On rejette donc, au seuil de , l'hypothèse d'un taux de satisfaction maintenu.