Les lois continues
Exercice 3 - Exercice 1
1 min
0
Les trois parties de cet exercice sont indépendantes.
Dans ce qui suit, les résultats approchés sont à arrondir au millième.
Une entreprise produit en grande série des clés USB pour l'industrie informatique.
Dans ce qui suit, les résultats approchés sont à arrondir au millième.
Une entreprise produit en grande série des clés USB pour l'industrie informatique.
Question 1
Partie A
On prélève au hasard clés dans la production de la journée pour vérification.
La production est assez grande pour que l'on puisse assimiler ce prélèvement à un tirage avec remise de clés.
On admet que la probabilité qu'une clé USB prélevée au hasard dans la production d'une journée soit défectueuse est égale à .
On considère la variable aléatoire qui, à tout prélèvement ainsi défini, associe le nombre de clés défectueuses de ce prélèvement.
On prélève au hasard clés dans la production de la journée pour vérification.
La production est assez grande pour que l'on puisse assimiler ce prélèvement à un tirage avec remise de clés.
On admet que la probabilité qu'une clé USB prélevée au hasard dans la production d'une journée soit défectueuse est égale à .
On considère la variable aléatoire qui, à tout prélèvement ainsi défini, associe le nombre de clés défectueuses de ce prélèvement.
Justifier que la variable aléatoire suit une loi binomiale dont on déterminera les paramètres.
Correction
Pour une clé, il n'y a que deux issues : elle est défectueuse, avec une probabilité , ou elle n'est pas défectueuse, avec la probabilité .
La production est assez grande pour que l'on puisse assimiler ce prélèvement à un tirage avec remise de 100 clés.
On peut en déduire que la variable aléatoire qui donne le nombre de clés défectueuses dans le lot de 100 clés suit la loi binomiale de paramètres et .
La production est assez grande pour que l'on puisse assimiler ce prélèvement à un tirage avec remise de 100 clés.
On peut en déduire que la variable aléatoire qui donne le nombre de clés défectueuses dans le lot de 100 clés suit la loi binomiale de paramètres et .
Question 2
Calculer les probabilités et
Correction
Pour le calcul de
Avec une Texas , on tape pour (cf. fiche Utiliser la loi binomiale avec une Texas)
2 - DISTR -- puis choisir
BinomFdp(valeur de n, valeur de p, valeur de k ) c'est-à-dire ici BinomFdp(, , ) puis taper sur enter et vous obtiendrez
Pour certaine version de Texas, on aura BinomPdf au lieu de BinomFdp
Avec une casio graph 35 + ou modèle supérieur , on tape pour ( Cf fiche utiliser la loi binomiale avec une Casio )
Choisir Menu Stat puis DIST puis BINM et prendre BPD puis VAR. On remplit le tableau de la manière qui suit
D.P. Binomiale
Data Variable
: Valeur de k
Numtrial : Valeur de
: Valeur de
puis taper sur EXE et vous obtiendrez
Pour le calcul de on effectue le même raisonnement. On donne directement le résultat. Ainsi
Avec une Texas , on tape pour (cf. fiche Utiliser la loi binomiale avec une Texas)
2 - DISTR -- puis choisir
BinomFdp(valeur de n, valeur de p, valeur de k ) c'est-à-dire ici BinomFdp(, , ) puis taper sur enter et vous obtiendrez
arrondi à près.
Pour certaine version de Texas, on aura BinomPdf au lieu de BinomFdp
Avec une casio graph 35 + ou modèle supérieur , on tape pour ( Cf fiche utiliser la loi binomiale avec une Casio )
Choisir Menu Stat puis DIST puis BINM et prendre BPD puis VAR. On remplit le tableau de la manière qui suit
D.P. Binomiale
Data Variable
: Valeur de k
Numtrial : Valeur de
: Valeur de
puis taper sur EXE et vous obtiendrez
arrondi à près.
Pour le calcul de on effectue le même raisonnement. On donne directement le résultat. Ainsi
Question 3
Calculer la probabilité que, dans un tel prélèvement, au plus deux clés soient défectueuses.
Correction
Au plus deux clés soient défectueuses correspond à l'événement .
La probabilité qu'au plus deux clés soient défectueuses est environ .
La probabilité qu'au plus deux clés soient défectueuses est environ .
Question 4
Partie B
Une clé est dite conforme pour la lecture lorsque sa vitesse de lecture, exprimée en Mo/s, appartient à l'intervalle .
Une clé est dite conforme pour l'écriture lorsque sa vitesse d'écriture exprimée en Mo/s appartient à l'intervalle .
Une clé est dite conforme pour la lecture lorsque sa vitesse de lecture, exprimée en Mo/s, appartient à l'intervalle .
Une clé est dite conforme pour l'écriture lorsque sa vitesse d'écriture exprimée en Mo/s appartient à l'intervalle .
On note la variable aléatoire qui, à chaque clé prélevée au hasard dans le stock, associe sa vitesse de lecture.
On suppose que la variable aléatoire suit la loi normale d'espérance et d'écart-type
Calculer la probabilité qu'une clé soit conforme pour la lecture.
On suppose que la variable aléatoire suit la loi normale d'espérance et d'écart-type
Calculer la probabilité qu'une clé soit conforme pour la lecture.
Correction
On note la variable aléatoire qui, à chaque clé prélevée au hasard dans le stock, associe sa vitesse de lecture.
On suppose que la variable aléatoire suit la loi normale d'espérance et d'écart-type
Une clé est conforme pour la lecture quand , sachant que la variable aléatoire suit la loi normale d'espérance et d'écart-type
La calculatrice donne
On suppose que la variable aléatoire suit la loi normale d'espérance et d'écart-type
Une clé est conforme pour la lecture quand , sachant que la variable aléatoire suit la loi normale d'espérance et d'écart-type
La calculatrice donne
.
Question 5
On note la variable aléatoire qui, chaque clé prélevée au hasard dans le stock, associe sa vitesse d'écriture.
On suppose que la variable aléatoire suit une loi normale.
Le graphique ci-après représente la densité de probabilité de la variable aléatoire .
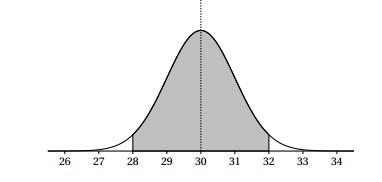
L'unité d'aire est choisie de façon à ce que l'aire sous la courbe soit égale à un et l'aire grisée est environ égale à unité d'aire.
La droite d'équation est un axe de symétrie de la courbe.
Déterminer l'espérance et l'écart-type de la variable aléatoire .
Justifier.
On suppose que la variable aléatoire suit une loi normale.
Le graphique ci-après représente la densité de probabilité de la variable aléatoire .

L'unité d'aire est choisie de façon à ce que l'aire sous la courbe soit égale à un et l'aire grisée est environ égale à unité d'aire.
La droite d'équation est un axe de symétrie de la courbe.
Déterminer l'espérance et l'écart-type de la variable aléatoire .
Justifier.
Correction
La fonction densité d'une loi normale d'espérance est représentée par une courbe en cloche dont l'axe de symétrie est la droite d'équation .
On sait que la droite d'équation est axe de symétrie donc on peut en déduire que .
On sait que la droite d'équation est axe de symétrie donc on peut en déduire que .
Si suit une loi normale de paramètre et alors :
D'après le texte, et on sait que ; donc et donc .Question 6
Partie C
Dans cette partie, on considère une grande quantité de clés devant être livrées à un éditeur de logiciels.
On considère un échantillon de clés prélevées au hasard dans cette livraison.
La livraison est assez importante pour que l'on puisse assimiler ce tirage à un tirage avec remise.
On constate que clés sont sans défaut.
Dans cette partie, on considère une grande quantité de clés devant être livrées à un éditeur de logiciels.
On considère un échantillon de clés prélevées au hasard dans cette livraison.
La livraison est assez importante pour que l'on puisse assimiler ce tirage à un tirage avec remise.
On constate que clés sont sans défaut.
Déterminer un intervalle de confiance, au niveau de confiance de 95%, de la proportion des clés USB qui sont sans défaut.
Correction
On constate que 94 clés sont sans défaut donc la fréquence de clés sans défaut dans cet échantillon est : .
Un intervalle de confiance, au niveau de confiance 95%, est donné par :
Un intervalle de confiance, au niveau de confiance 95%, est donné par :
- , que l'on remplacera par 1 car une probabilité ne peut dépasser 1.