La fonction logarithme
QCM - Exercice 1
20 min
35
On considère la fonction définie sur l’intervalle par : .
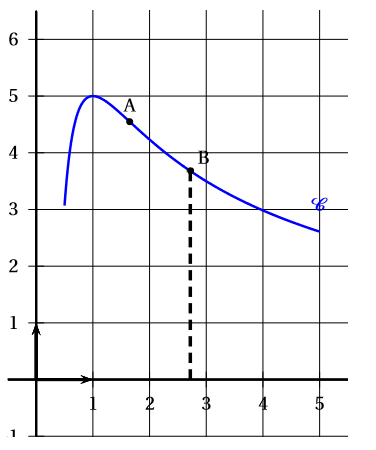
Sa représentation graphique est la courbe donnée ci-dessous dans un repère d’origine . On admet que le point placé sur le graphique est le seul point d’inflexion de la courbe sur l’intervalle . On note le point de cette courbe d’abscisse . On admet que la fonction est deux fois dérivable sur cet intervalle. On rappelle que désigne la fonction dérivée dela fonction et sa fonction dérivée seconde.
Sa représentation graphique est la courbe donnée ci-dessous dans un repère d’origine . On admet que le point placé sur le graphique est le seul point d’inflexion de la courbe sur l’intervalle . On note le point de cette courbe d’abscisse . On admet que la fonction est deux fois dérivable sur cet intervalle. On rappelle que désigne la fonction dérivée dela fonction et sa fonction dérivée seconde.
Question 1
La fonction est :
- positive ou nulle sur l’intervalle
- négative ou nulle sur l’intervalle
- négative ou nulle sur l’intervalle
- positive ou nulle sur l’intervalle
- négative ou nulle sur l’intervalle
- négative ou nulle sur l’intervalle
Correction
La bonne réponse est .
Pour tout réel appartenant à , on vérifie aisément que . Il en résulte donc que le signe de dépend de .
Il en résulte donc que :

Pour tout réel appartenant à , on vérifie aisément que . Il en résulte donc que le signe de dépend de .
Il en résulte donc que :
- si alors .
- si alors .

Question 2
Le coefficient directeur de la tangente à la courbe au point est égal à :
-
-
-
Correction
La bonne réponse est .
On rappelle que l'abscisse du point est .
Pour déterminer le coefficient directeur de la tangente à la courbe au point , il nous faut calculer .
Nous savons que . Il vient alors que :
On rappelle que l'abscisse du point est .
Pour déterminer le coefficient directeur de la tangente à la courbe au point , il nous faut calculer .
Nous savons que . Il vient alors que :
Question 3
La fonction est :
- croissante sur l’intervalle
- décroissante sur l’intervalle
- croissante sur l’intervalle
- croissante sur l’intervalle
- décroissante sur l’intervalle
- croissante sur l’intervalle
Correction
La bonne réponse est .
Il nous faut ici étudier le signe de qui nous permettra d'avoir les variations de .
Pour tout réel appartenant à , on vérifie aisément que . Il en résulte donc que le signe de dépend de .
Or .
Il en résulte donc que :
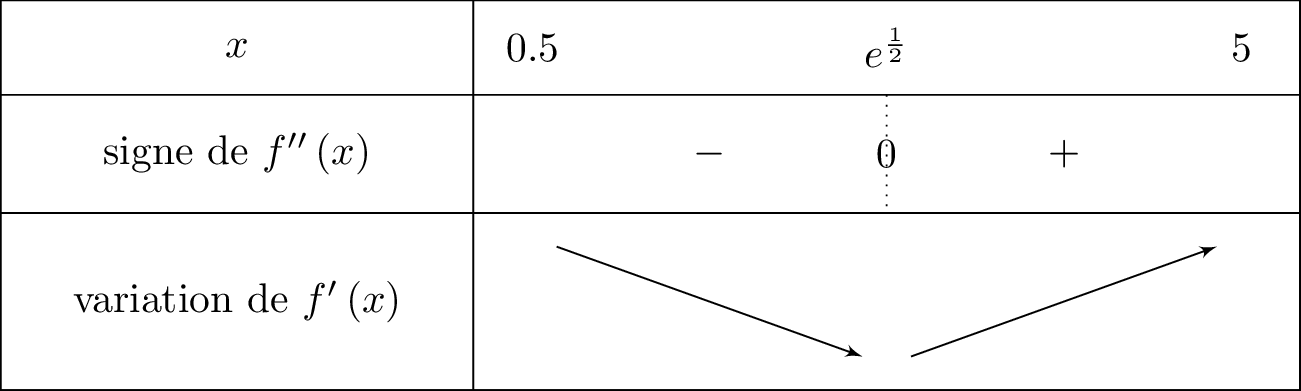
Il nous faut ici étudier le signe de qui nous permettra d'avoir les variations de .
Pour tout réel appartenant à , on vérifie aisément que . Il en résulte donc que le signe de dépend de .
Or .
Il en résulte donc que :
- si alors et donc la fonction est décroissante sur cet intervalle.
- si alors et donc la fonction est croissante sur cet intervalle.

Question 4
La valeur exacte de l’abscisse du point de la courbe est égale à :
Correction
La bonne réponse est .
Le point ici correspond au point d'inflexion.
Il en résulte donc alors que :
équivaut successivement à :
. Or ici, nous savons que et de ce fait .
Il vient alors que :
équivaut successivement à :
Le point ici correspond au point d'inflexion.
Il en résulte donc alors que :
équivaut successivement à :
. Or ici, nous savons que et de ce fait .
Il vient alors que :
équivaut successivement à :
Question 5
On note l’aire, mesurée en unités d’aire, du domaine plan délimité par la courbe , l’axe des abscisses et les droites d’équation et . Cette aire vérifie :
-
-
-
Correction
La fonction est positive sur donc l'intégrale est positive et est égale à l'aire sous la courbe et l'axe des abscisses et délimité par les droites verticales et .
Il suffit de compter les nombres de carreaux sous la courbe et l'axe des abscisses et délimité par les droites verticales et .
Il y a plus de dix carreaux mais moins de quinze carreaux.
D'où :
Il suffit de compter les nombres de carreaux sous la courbe et l'axe des abscisses et délimité par les droites verticales et .
Il y a plus de dix carreaux mais moins de quinze carreaux.
D'où :