La fonction logarithme
Exercices types : ème partie - Exercice 1
15 min
20
Question 1
Soit la fonction définie sur , par .
La courbe est la représentation graphique de la fonction sur l’intervalle .
La courbe est la représentation graphique de la fonction sur l’intervalle .
Montrer que .
Correction
On reconnait la forme : avec et .
Ainsi : et .
Il vient alors que :
Ainsi : et .
Il vient alors que :
Question 2
Dresser le tableau de variation de sur . On ne vous demande pas de compléter les valeurs dans le tableau.
Correction
Pour tout réel , on vérifie aisément que . Donc le signe de dépend de .
Ainsi :
équivaut successivement à :
.
Cela signifie que l'on mettra le signe pour le signe de dès que .
Nous allons maintenant dresser le tableau de variation de .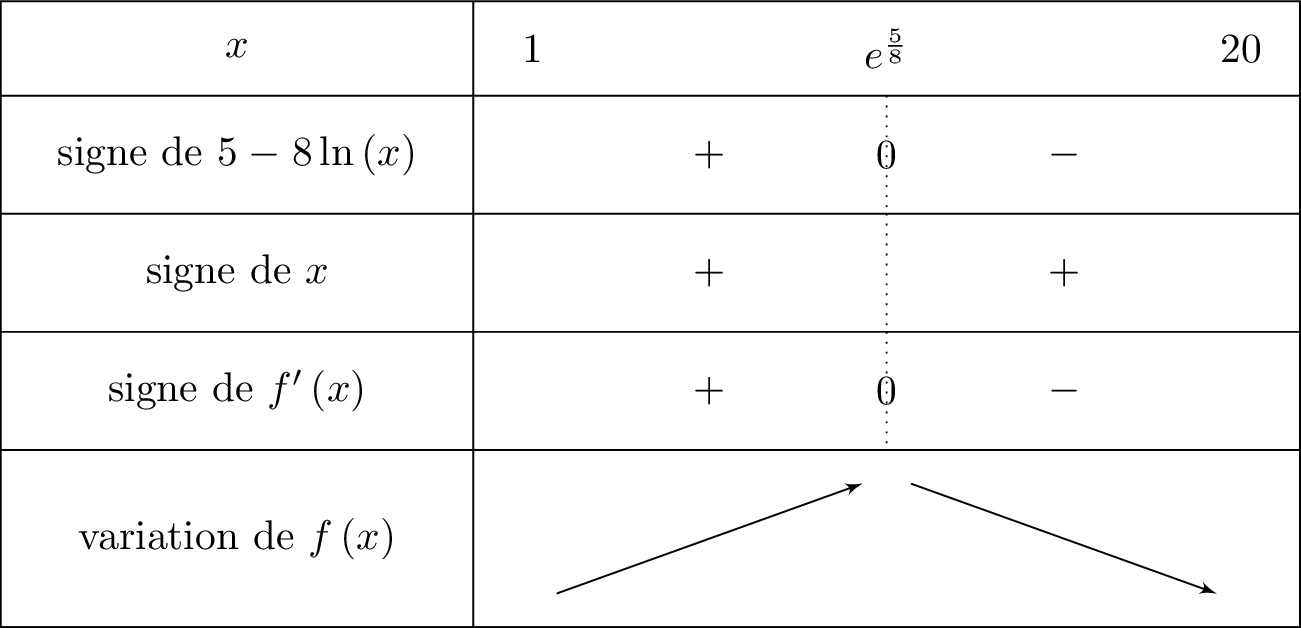
Ainsi :
équivaut successivement à :
.
Cela signifie que l'on mettra le signe pour le signe de dès que .
Nous allons maintenant dresser le tableau de variation de .

Question 3
Calculer la dérivée de que l'on note .
Correction
Nous savons que
On reconnait la forme : avec et .
Ainsi : et .
Il vient alors que :
Ainsi :
On reconnait la forme : avec et .
Ainsi : et .
Il vient alors que :
Ainsi :
Question 4
Etudier la convexité de la fonction sur l'intervalle .
Correction
Pour étudier la convexité de la fonction , il faut étudier le signe de .
Nous savons que
Pour tout réel appartenant à l'intervalle comme alors est du signe de .
Pour étudier son signe on résout l'inéquation , il vient alors :
équivaut successivement à :
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera supérieur ou égale à .
Il en résulte :
- Lorsque sur un intervalle alors est convexe.
- Lorsque sur un intervalle alors est concave.
Pour tout réel appartenant à l'intervalle comme alors est du signe de .
Pour étudier son signe on résout l'inéquation , il vient alors :
équivaut successivement à :
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera supérieur ou égale à .
Il en résulte :
