La fonction logarithme
Exercices types : ème partie - Exercice 1
30 min
45
Partie A.
Question 1
Soit la fonction définie sur par : . On note la courbe représentative de la fonction .
Montrer que sur l'intervalle , on a :
Correction
est dérivable sur .
Ici on reconnaît la forme : avec ; et
Ainsi : ; et .
Il vient alors que :
équivaut successivement à :
Ici on reconnaît la forme : avec ; et
Ainsi : ; et .
Il vient alors que :
équivaut successivement à :
Question 2
Etudier les variations de la fonction sur .
Correction
Il nous faut ici calculer puis étudier le signe de . Nous pourrons ainsi obtenir les variations de .
Nous savons que et est dérivable sur .
Ainsi :
Pour tout , on vérifie aisément que et de ce fait le signe de dépend de .
Or :
Il en résulte donc que lorsque .
Nous allons traduire ces informations dans le tableau de variation ci-dessous :
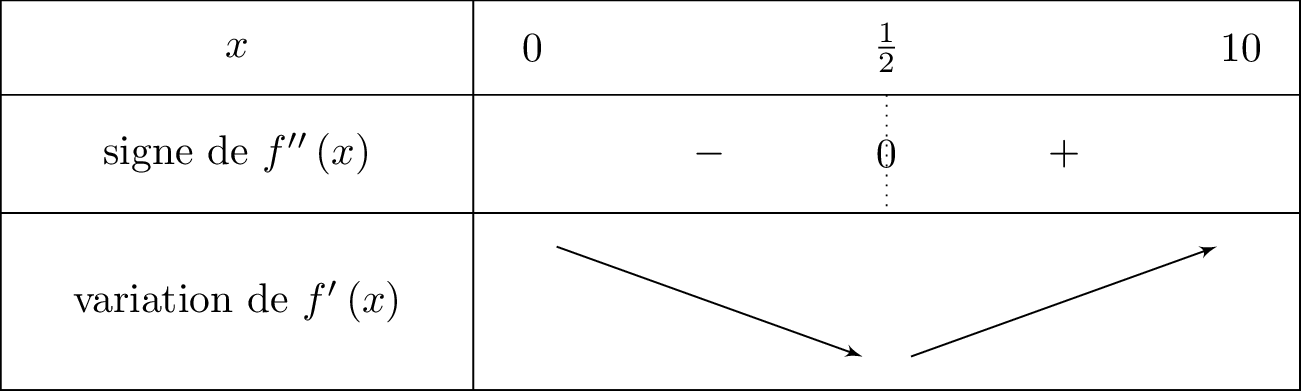
Nous savons que et est dérivable sur .
Ainsi :
Pour tout , on vérifie aisément que et de ce fait le signe de dépend de .
Or :
Il en résulte donc que lorsque .
Nous allons traduire ces informations dans le tableau de variation ci-dessous :

Question 3
En déduire les variations de .
Correction
D'après la question , nous connaissons le tableau de variation de . De plus, la fonction admet un minimum lorsque .
Calculons la valeur de ce minimum.
Il vient alors que :
. Comme
Ainsi :
Il en résulte donc que le minimum de est strictement positif. On peut donc conclure que la fonction est strictement positive sur et de ce fait la fonction est strictement croissante sur .
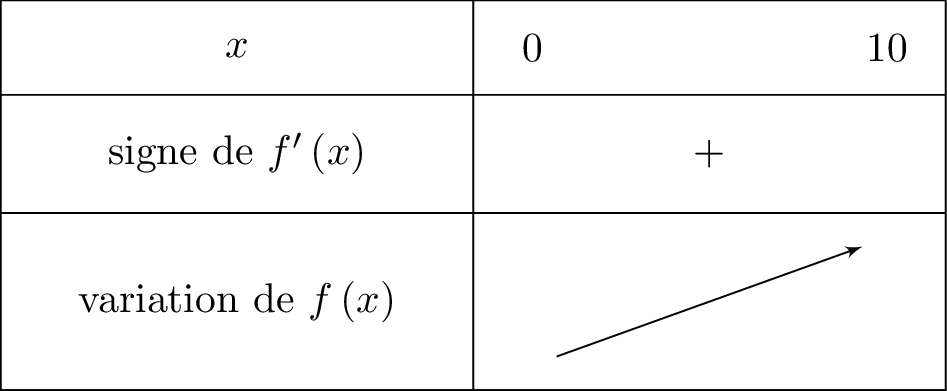
Calculons la valeur de ce minimum.
Il vient alors que :
. Comme
Ainsi :
Il en résulte donc que le minimum de est strictement positif. On peut donc conclure que la fonction est strictement positive sur et de ce fait la fonction est strictement croissante sur .

Question 4
Partie B.
Une entreprise produit et commercialise les protections (coques) pour téléphone haut de gamme. Sa capacité de production est comprise entre et coques par jour. Le coût total de production exprimé en milliers d'euros est modélisé sur l'intervalle par la fonction de la partie , où désigne le nombre de milliers d'articles fabriqués.
Soit le coût moyen de production exprimé en euros, par article fabriqué.
La fonction est définie sur par
Une entreprise produit et commercialise les protections (coques) pour téléphone haut de gamme. Sa capacité de production est comprise entre et coques par jour. Le coût total de production exprimé en milliers d'euros est modélisé sur l'intervalle par la fonction de la partie , où désigne le nombre de milliers d'articles fabriqués.
Soit le coût moyen de production exprimé en euros, par article fabriqué.
La fonction est définie sur par
On note la dérivée de sur . Calculer .
Correction
Soit . est dérivable sur .
Ainsi : . Nous allons décomposer afin de calculer plus facilement la dérivée.
On a :
Maintenant, nous allons calculer .
Ainsi : . Nous allons décomposer afin de calculer plus facilement la dérivée.
On a :
Maintenant, nous allons calculer .
Question 5
Étudier les variations de la fonction sur l'intervalle . Donner le tableau de variation complet.
Correction
Nous savons que .
Comme , alors . Le signe de est alors de son numérateur .
Il s'agit d'une équation du second degré. Nous allons utiliser le discriminant.
Or : donc .
Il existe donc deux racines réelles distinctes.
De plus :
donc
donc
donc
On en déduit le tableau de variation suivant :
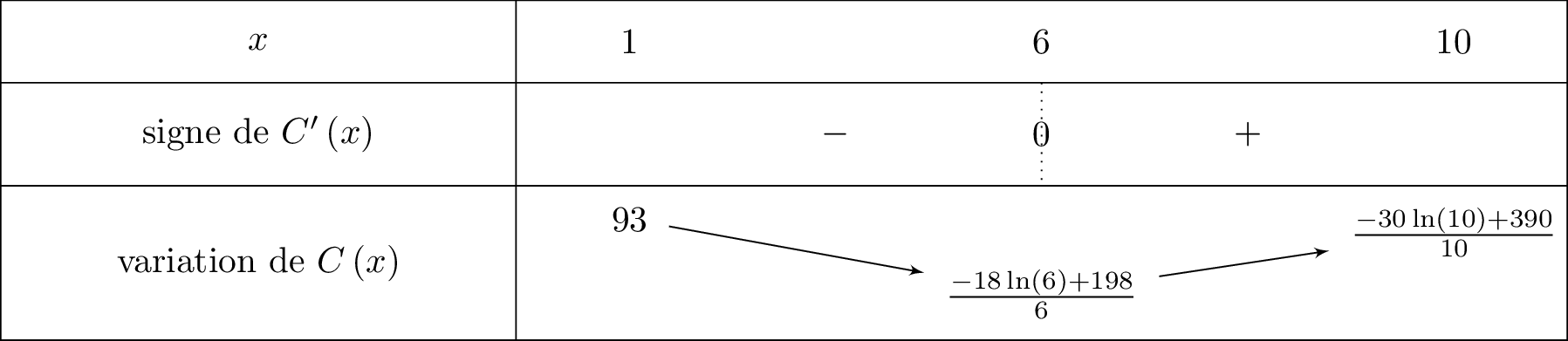
Comme , alors . Le signe de est alors de son numérateur .
Il s'agit d'une équation du second degré. Nous allons utiliser le discriminant.
Or : donc .
Il existe donc deux racines réelles distinctes.
- ce qui donne .
- ce qui donne .
De plus :
donc
donc
donc
On en déduit le tableau de variation suivant :

Question 6
Montrer que l'équation admet une unique solution sur l'intervalle . Donner un encadrement de à près.
Correction
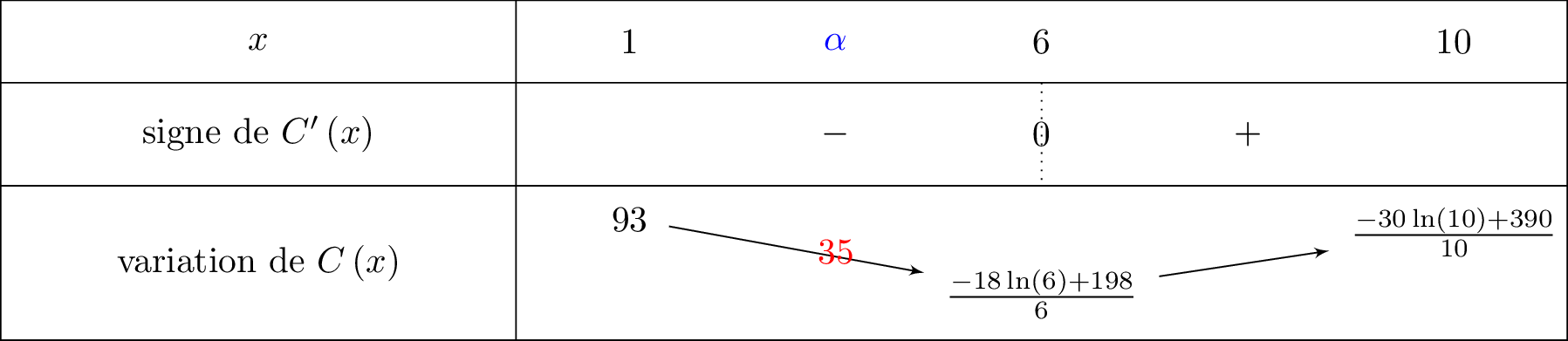
- Sur , la fonction est continue et admet comme maximum.
Donc l'équation n'a pas de solution sur cet intervalle. - Sur , la fonction est continue et strictement décroissante.
De plus, et
Or , donc d'après le théorème des valeurs intermédiaires, il existe une unique solution dans tel que
Question 7
Donner un encadrement de à près.
Correction
A la calculatrice, on vérifie que :
et .
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
et .
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :