La fonction logarithme
Exercices types : ère partie - Exercice 1
25 min
35
Question 1
Soit la fonction définie sur par . On note la courbe représentative de la fonction .
Calculer .
Correction
est dérivable sur . Il vient alors que :
. Nous allons tout mettre au même dénominateur.
Ainsi :
. Nous allons tout mettre au même dénominateur.
Ainsi :
Question 2
Dresser le tableau de variation de .
Correction
On sait que :
Pour tout appartenant à , on a , donc le signe de est alors du signe de .
Pour étudier le signe de , nous allons utiliser le discriminant.
Ainsi : ; et
, la parabole est tournée vers le haut c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
De plus : c'est à dire
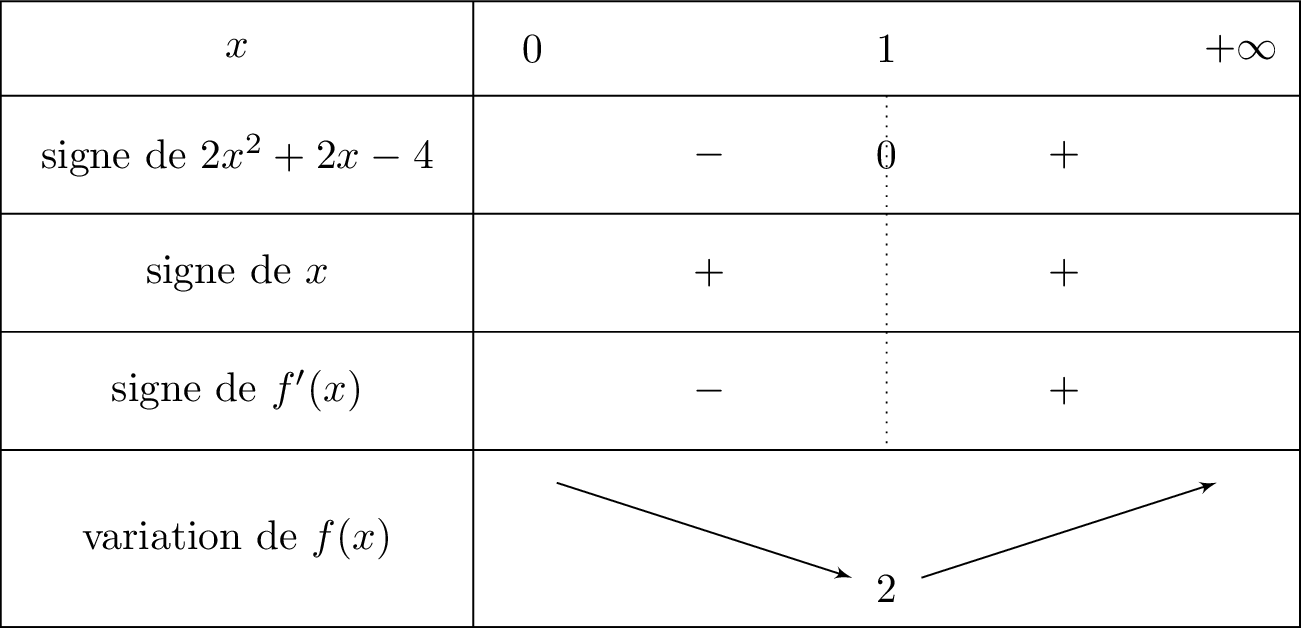
On en déduit le tableau de variation suivant :
Pour tout appartenant à , on a , donc le signe de est alors du signe de .
Pour étudier le signe de , nous allons utiliser le discriminant.
Ainsi : ; et
, la parabole est tournée vers le haut c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
De plus : c'est à dire
On en déduit le tableau de variation suivant :

Question 3
En déduire le signe de .
Correction
Sur l'intervalle , la courbe admet un minimum qui vaut lorsque .
Il en résulte donc que la fonction est strictement positive sur . Le tableau de signe de est donnée ci-dessous:

Il en résulte donc que la fonction est strictement positive sur . Le tableau de signe de est donnée ci-dessous:

Question 4
Etudiez la convexité de .
Correction
Pour étudier la convexité de la fonction , il faut étudier le signe de .
Sur l'intervalle , on sait que :
On reconnaît la forme avec et
Ainsi : et .
Il vient alors que :
Pour tout appartenant à , on a : et . Il en résulte que : sur l'intervalle .

- Lorsque sur un intervalle alors est convexe.
- Lorsque sur un intervalle alors est concave.
On reconnaît la forme avec et
Ainsi : et .
Il vient alors que :
Pour tout appartenant à , on a : et . Il en résulte que : sur l'intervalle .

Question 5
Déterminer une équation de la tangente à la courbe au point d'abscisse .
Correction
L'équation de la tangente au point d'abscisse s'écrit .
Ici , ce qui donne, .1ère étape : calculer
2ème étape : calculer
3ème étape : on remplace les valeurs de et de dans la formule de l'équation de tangente.
On sait que :
Ainsi l'équation de la tangente à la courbe au point d'abscisse est alors :
.