La fonction logarithme

Exercice 6 - Exercice 1

1 min
0
Les parties A et B de cet exercice sont indépendantes.
On considère la fonction ff définie sur [14;5]\left[\frac{1}{4} ;5\right] dont on donne la représentation graphique (C)\left(C\right) dans le repère ci-dessous.

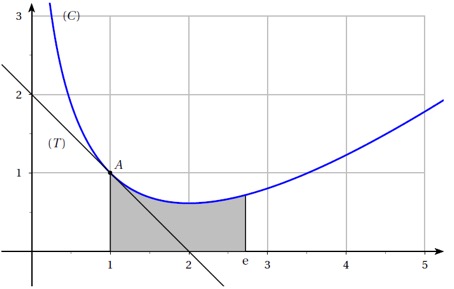
On admet que :
  • Le point AA de coordonnées (1;1)\left(1;1\right) appartient à la courbe (C)\left(C\right)
  • La tangente (T)\left(T\right) en AA à la courbe (C)\left(C\right) passe par le point de coordonnées (2;0)\left(2;0\right);
  • La courbe (C)\left(C\right) admet une tangente horizontale au point d'abscisse 22 ;
L'axe des ordonnées est asymptote à la courbe de la fonction ff .
Question 1
Partie A

Donner, par lecture graphique ou en utilisant les données de l'énoncé, les valeurs de f(1)f\left(1\right), f′(1)f'\left({\text 1}\right), et f′(2)f'\left({\text 2}\right), où f′f' est la fonction dérivée de ff sur [14;5]\left[\frac{1}{4} ;5\right].

Correction
On a :
  • f(1)=1f\left(1\right)=1.
  • f′(2)=0f'\left(2\right)=0 car la tangente au point d'abscisse 2 est horizontale.
  • f′(1)f'\left(1\right) est le coefficient directeur de la tangente au point AA.
    La tangente passe donc par le point A(1;1)A\left(1;1\right) et par le point (0;2)\left(0;2\right) que l'on appelle DD .
    Ainsi : f′(1)=yD−yAxD−xA=0−12−1f'\left(1\right)=\frac{y_{D} -y_{A} }{x_{D} -x_{A} } =\frac{0-1}{2-1} donc f′(1)=−1f'\left(1\right)=-1.
Question 2
On admet que l'expression de ff sur [14;5]\left[\frac{1}{4} ;5\right] est : f(x)=ax+b+cln⁡xf\left(x\right)=ax+b+c\ln x où aa, bb et cc sont des nombres réels.

Calculer f′(x)f'\left(x\right) en fonction de xx et de aa, bb et cc.

Correction
ff est dérivable sur [14;5]\left[\frac{1}{4} ;5\right], on a :
f′(x)=a+c×1xf'\left(x\right)=a+c\times \frac{1}{x}
f′(x)=a+cxf'\left(x\right)=a+\frac{c}{x}
Question 3

Démontrer que les réels aa, bb et cc vérifient le système {a+b=1a+c=−1a+c2=0\left\{\begin{array}{ccccc} {a} & {+} & {b} & {=} & {1} \\ {a} & {+} & {c} & {=} & {-1} \\ {a} & {+} & {\frac{c}{2} } & {=} & {0} \end{array}\right.

Correction
  • f(1)=1f\left(1\right)=1 ce qui implique que a+b+cln⁡(1)=1a+b+c\ln \left(1\right)=1, on a donc
    a+b=1a+b=1
  • f′(1)=−1f'\left({\text 1}\right)=-1 ce qui implique que a+c1=−1a+\frac{c}{1} =-1, on a donc
    a+c=−1a+c=-1
  • f′(2)=0f'\left({\text 2}\right)=0 ce qui implique que a+c2=0a+\frac{c}{2} =0, on a donc
    a+c2=0a+\frac{c}{2} =0

Ainsi les réels aa, bb et cc vérifient le système {a+b=1a+c=−1a+c2=0\left\{\begin{array}{ccccc} {a} & {+} & {b} & {=} & {1} \\ {a} & {+} & {c} & {=} & {-1} \\ {a} & {+} & {\frac{c}{2} } & {=} & {0} \end{array}\right.
Question 4

Déduire de la question précédente les valeurs de aa, bb et cc puis l'expression de f(x)f\left(x\right).

Correction
On a :
{a+b=1a+c=−1a+c2=0\left\{\begin{array}{ccccc} {a} & {+} & {b} & {=} & {1} \\ {a} & {+} & {c} & {=} & {-1} \\ {a} & {+} & {\frac{c}{2} } & {=} & {0} \end{array}\right.
Nous allons multiplier la 33ème par 22, ainsi :
{a+b=1a+c=−12a+c=0\left\{\begin{array}{ccccc} {a} & {+} & {b} & {=} & {1} \\ {a} & {+} & {c} & {=} & {-1} \\ {2a} & {+} & {c} & {=} & {0} \end{array}\right.
Ensuite, toujours avec la 33ème ligne, on va exprimer cc en fonction de aa.
{a+b=1a+c=−1c=−2a\left\{\begin{array}{ccccc} {a} & {+} & {b} & {=} & {1} \\ {a} & {+} & {c} & {=} & {-1} \\ {} & {} & {c} & {=} & {-2a} \end{array}\right.
On va maintenant remplacer dans la 22ème ligne le fait que c=−2ac=-2a.
{a+b=1a+−2a=−1c=−2a\left\{\begin{array}{ccccc} {a} & {+} & {b} & {=} & {1} \\ {a} & {+} & {-2a} & {=} & {-1} \\ {} & {} & {c} & {=} & {-2a} \end{array}\right.
{a+b=1−a=−1c=−2a\left\{\begin{array}{ccccc} {a} & {+} & {b} & {=} & {1} \\ {} & {} & {-a} & {=} & {-1} \\ {} & {} & {c} & {=} & {-2a} \end{array}\right.
{a+b=1a=1c=−2a\left\{\begin{array}{ccccc} {a} & {+} & {b} & {=} & {1} \\ {} & {} & {a} & {=} & {1} \\ {} & {} & {c} & {=} & {-2a} \end{array}\right.
{a+b=1a=1c=−2\left\{\begin{array}{ccccc} {a} & {+} & {b} & {=} & {1} \\ {} & {} & {a} & {=} & {1} \\ {} & {} & {c} & {=} & {-2} \end{array}\right.
{b=1−aa=1c=−2\left\{\begin{array}{ccc} {b} & {=} & {1-a} \\ {a} & {=} & {1} \\ {c} & {=} & {-2} \end{array}\right.
{b=0a=1c=−2\left\{\begin{array}{ccc} {b} & {=} & {0} \\ {a} & {=} & {1} \\ {c} & {=} & {-2} \end{array}\right.
Comme f(x)=ax+b+cln⁡xf\left(x\right)=ax+b+c\ln x alors f(x)=x−2ln⁡xf(x)=x-2\ln x.
Question 5
Partie B
Dans cette partie, on admet que la fonction ff représentée ci-dessus est définie pour tout réel xx appartenant à [14;5]\left[\frac{1}{4} ;5\right] par : f(x)=x−2ln⁡xf(x)=x-2\ln x

Calculer la dérivée g′g' de la fonction gg définie pour tout réel x∈[14;5]x\in \left[\frac{1}{4} ;5\right] par : g(x)=xln⁡x−xg(x)=x\ln x-x. Que peut-on en déduire?

Correction
On reconnait la forme (uv)′=u′v+uv′\left(uv\right)'=u'v+uv' avec u(x)=xu\left(x\right)=x et v(x)=ln⁡xv\left(x\right)=\ln x.
Ainsi u′(x)=1u'\left(x\right)=1 et v′(x)=1xv'\left(x\right)=\frac{1}{x} .
On a alors :
g′(x)=ln⁡x+x×1x−1g'\left(x\right)=\ln x+x\times \frac{1}{x} -1
g′(x)=ln⁡x+1−1g'\left(x\right)=\ln x+1-1
g′(x)=ln⁡xg'\left(x\right)=\ln x

La fonction xln⁡x−xx\ln x-x est donc une primitive de la fonction ln⁡x\ln x.
Question 6

En déduire une primitive FF de la fonction ff sur[14;5]\left[\frac{1}{4} ;5\right].

Correction
On sait que :
f(x)=x−2ln⁡xf(x)=x-2\ln x
D'où :
F(x)=x22−2(xln⁡x−x)F\left(x\right)=\frac{x^{2} }{2} -2\left(x\ln x-x\right)
Question 7

Déterminer la valeur exacte, en unités d'aire, de l'aire du domaine grisé sur le graphique ci-dessus, délimité par la courbe (C)\left(C\right), l'axe des abscisses et les droites d'équation x=1x=1 et x=ex=e.

Correction
La fonction ff est positive sur l'intervalle [1;e]\left[1;e\right], donc l'aire de la surface du domaine est égale à l'intégrale :
∫1ef(x)dx=F(e)−F(1)\int _{1}^{e}f\left(x\right)dx =F\left(e\right)-F\left(1\right) équivaut successivement à
∫1ef(x)dx=e22−2(eln⁡e−e)−[12−2(1ln⁡1−1)]\int _{1}^{e}f\left(x\right)dx =\frac{e^{2} }{2} -2\left(e\ln e-e\right)-\left[\frac{1}{2} -2\left(1\ln 1-1\right)\right]
∫1ef(x)dx=e22−2e+2e−12−2\int _{1}^{e}f\left(x\right)dx =\frac{e^{2} }{2} -2e+2e-\frac{1}{2} -2
∫1ef(x)dx=e22−52\int _{1}^{e}f\left(x\right)dx =\frac{e^{2} }{2} -\frac{5}{2}
∫1ef(x)dx≈1,2\int _{1}^{e}f\left(x\right)dx \approx 1,2