La fonction logarithme

Exercice 5 - Exercice 1

1 min
0
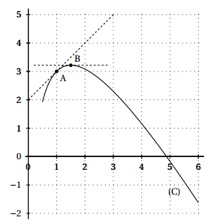
La courbe (C)\left(C\right) ci-dessous représente, dans un repère orthonormé, une fonction ff définie et dérivable sur B(0;−1)B\left(0;-1\right).
Les points A(1;3)A\left(1;3\right) et BB d'abscisse 1,51,5 sont sur la courbe (C)\left(C\right).
Les tangentes à la courbe (C)\left(C\right) aux points AA et BB sont aussi représentées en pointillés sur ce graphique, la tangente au point BB est horizontale.
On note f′f' la fonction dérivée de ff.
Les parties AA et BB sont indépendantes.
Question 1
Partie AA : Etude graphique

Déterminer f′(1,5)f'(1,5).

Correction
f′(1,5)=0f'(1,5)=0 car au point BB d'abscisse 1,51,5 la tangente à (C)\left(C\right) est horizontale.
Question 2

La tangente à la courbe (C)\left(C\right) passant par A, passe par le point de coordonnées (0;2)\left(0;2\right).
Déterminer une équation de cette tangente.

Correction
On veut déterminer l'équation de la tangente au point d'abscisse 11.
Appelons le point II de coordonnées (0;2)\left(0;2\right).
La tangente passe alors par les points II et AA.
Le coefficient directeur de cette tangente est :
f′(1)=yI−yAxI−xAf '(1)=\frac{y_{I} -y_{A} }{x_{I} -x_{A} }
f′(1)=2−30−1f'(1)=\frac{2-3}{0-1}
f′(1)=1f '(1)=1

De plus f(1)=3f(1)=3
On a donc :
y=f′(1)(x−1)+f(1)y=f '(1)\left(x-1\right)+f\left(1\right)
y=1(x−1)+3y=1\left(x-1\right)+3
Finalement la tangente à (C)\left(C\right) en AA, a pour équation
y=x+2y=x+2
Question 3

Donner un encadrement de l'aire, en unités d'aire et à l'unité près, du domaine compris entre la courbe (C)\left(C\right), l'axe des abscisses et les droites d'équation x=1x=1 et x=2x=2.

Correction
La fonction est positive sur [1;2]\left[1;2\right] donc l'aire cherchée est donnée par A=∫12f(x)dxA=\int _{1}^{2}f(x)dx .
On compte 33 carreaux minimum et 44 carreaux maximum sous la courbe et les droites d'équations verticales x=1x=1 et x=2x=2.
On a :
3≤A≤43\le A\le 4
Question 4

Déterminer la convexité de la fonction ff sur B(0;−1)B\left(0;-1\right).
Argumenter la réponse.

Correction
La courbe est concave sur B(0;−1)B\left(0; -1\right) car elle se situe en tout point en dessous de sa tangente.
Question 5
Partie B : Etude analytique
On admet que la fonction ff est définie sur [0,5;6]\left[0,5;6\right] par : f(x)=−2x+5+3ln⁡(x)f\left(x\right)=-2x+5+3\ln \left(x\right)

Pour tout réel xx de [0,5;6]\left[0,5;6\right], calculer f′(x)f'\left(x\right) et montrer que f′(x)=−2x+3xf'\left(x\right)=\frac{-2x+3}{x} .

Correction
ff est une somme de fonctions dérivables sur [0,5;6]\left[0,5;6\right], donc elle est dérivable sur cet intervalle.
Pour tout réel x∈[0,5;6]x\in \left[0,5;6\right], on a :
f′(x)=−2+3xf'\left(x\right)=-2+\frac{3}{x} .
On va tout mettre au même dénominateur.
f′(x)=−2x+3xf'\left(x\right)=\frac{-2x+3}{x}
Question 6

Etudier le signe de f′f' sur B(0;−1)B\left(0;-1\right) puis dresser le tableau de variation de ff sur B(0;−1)B\left(0;-1\right).

Correction
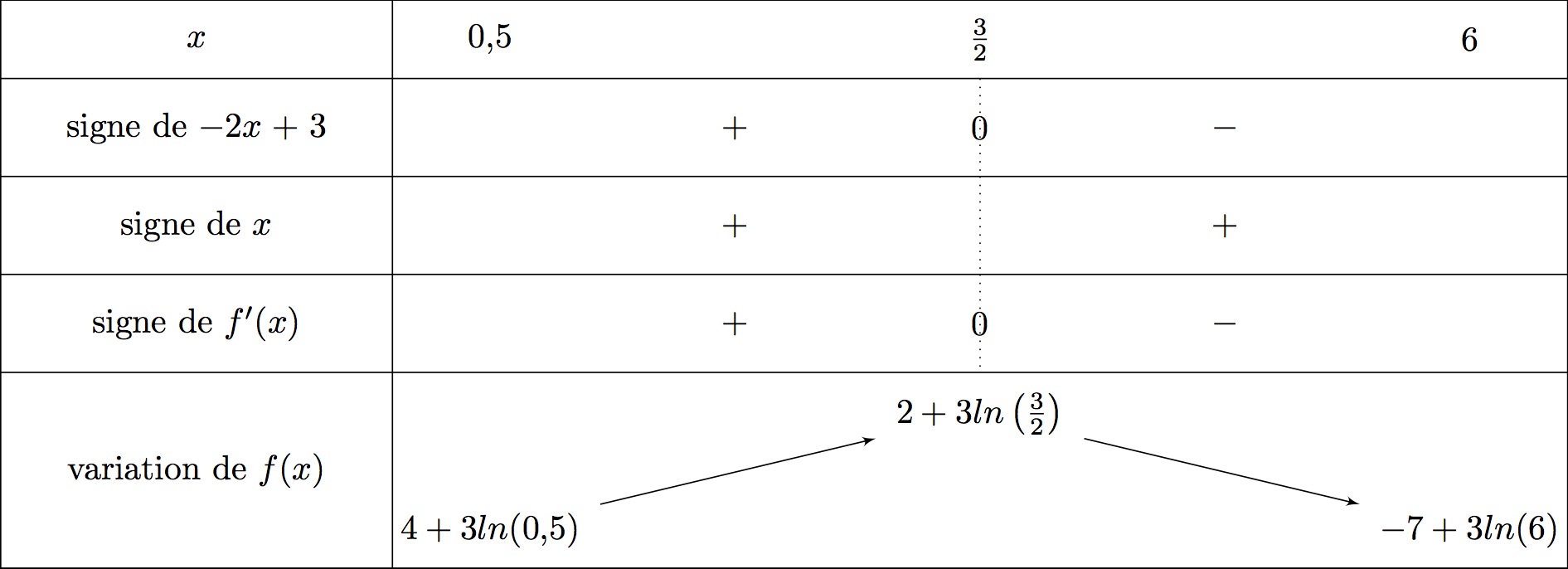
Sur B(0;−1)B\left(0; -1\right), x>0x>0 donc f′(x)f'(x) est du signe de −2x+3-2x+3.
−2x+3≥0-2x+3\ge 0 équivaut successivement à
−2x≥−3-2x\ge -3
x≤−3−2x\le \frac{-3}{-2}
x≤32x\le \frac{3}{2}
Il en résulte donc que :
  • si x∈[0,5;32]x\in\left[0,5;\frac{3}{2}\right] alors f′(x)≥0f'\left(x\right)\ge0 et donc ff est croissante sur cet intervalle.
  • si x∈[32;6]x\in\left[\frac{3}{2};6\right] alors f′(x)≤0f'\left(x\right)\le0 et donc ff est décroissante sur cet intervalle.
On en déduit le tableau de variation suivant

  • f(0,5)=−2×0,5+5+3ln⁡(0,5)=4+3ln⁡(0,5)f\left(0,5\right)=-2\times 0,5+5+3\ln \left(0,5\right)=4+3\ln \left(0,5\right) donc f(0,5)≈1,92f\left(0,5\right)\approx 1,92
  • f(32)=−2×32+5+3ln⁡(32)=2+3ln⁡(32)f\left(\frac{3}{2} \right)=-2\times \frac{3}{2} +5+3\ln \left(\frac{3}{2} \right)=2+3\ln \left(\frac{3}{2} \right) donc f(32)≈2,40f\left(\frac{3}{2} \right)\approx 2,40
  • f(6)=−2×6+5+3ln⁡(6)=−7+3ln⁡(6)f\left(6\right)=-2\times 6+5+3\ln \left(6\right)=-7+3\ln \left(6\right) donc f(6)≈−1,62f\left(6\right)\approx -1,62
Question 7

Montrer que l'équation f(x)=0f(x)=0 admet exactement une solution α\alpha sur B(0;−1)B\left(0;-1\right).
Donner une valeur approchée de α\alpha à 10−210^{-2} près.

Correction
  • Sur [0,5;32]\left[0,5;\frac{3}{2} \right], la fonction ffest continue et admet 4+3ln⁡(0,5)>04+3\ln \left(0,5\right)>0 comme minimum.
    La fonction ff est strictement positive.
    Donc l'équation f(x)=0f\left(x\right)=0 n'a pas de solution sur cet intervalle.
  • Sur [32;6]\left[\frac{3}{2} ;6\right], la fonction ff est continue et strictement décroissante.
    De plus, f(32)=2+3ln⁡(32)f\left(\frac{3}{2} \right)=2+3\ln \left(\frac{3}{2} \right)et f(6)=−7+3ln⁡(6)f\left(6\right)=-7+3\ln \left(6\right) .
    Or 0∈[−7+3ln⁡(6);2+3ln⁡(32)]0\in \left[-7+3\ln \left(6\right);2+3\ln \left(\frac{3}{2} \right)\right], donc d'après le théorème des valeurs intermédiaires, il existe une unique solution α\alpha dans B(0;−1)B\left(0; -1\right) tel que f(x)=0f\left(x\right)=0.

A la calculatrice, on vérifie que :
f(4,876)≈0,00097f\left(4,876\right)\approx 0,00097 et f(4,878)≈−0,0004f\left(4,878\right)\approx -0,0004 .
Or 0∈]−0,0004;0,00097]0\in \left]-0,0004;0,00097\right], donc d'après le théorème des valeurs intermédiaires on en déduit que
α≈4,88\alpha \approx 4,88
Question 8

En déduire le tableau de signe de ff sur B(0;−1)B\left(0;-1\right).

Correction
Sur [0,5;32]\left[0,5;\frac{3}{2} \right], la fonction ffest continue et admet 4+3ln⁡(0,5)>04+3\ln \left(0,5\right)>0 comme minimum.
La fonction ff est strictement positive.
Sur [32;6]\left[\frac{3}{2} ;6\right], la fonction ff est continue et strictement décroissante et f(α)=0f\left(\alpha \right)=0.
Donc f(x)≥0f\left(x\right)\ge 0 pour tout x∈[0,5;α]x\in \left[0,5;\alpha \right] et f(x)≤0f\left(x\right)\le 0 pour tout x∈[α;6]x\in \left[\alpha ;6\right].
On résume cela dans un tableau de signe :
Question 9
On considère la fonction FF définie sur B(0;−1)B\left(0;-1\right) par F(x)=−x2+2x+3xln⁡(x)F(x)=-x^{2} +2x+3x\ln (x).

Montrer que FF est une primitive de ff sur B(0;−1)B\left(0;-1\right).

Correction
FF est dérivable sur[0,5;6]\left[0,5;6\right] comme somme et produit de fonctions dérivables sur [0,5;6]\left[0,5;6\right].
Dans le cas où une primitive FF est donnée, il vous suffit de dériver FF et d'obtenir comme résultat ff.
Autrement dit, il faut que : F′(x)=f(x)F'\left(x\right)=f\left(x\right)
On reconnaît la forme (uv)′=u′v+uv′\left(uv\right)^{'} =u'v+uv' avec u(x)=3xu\left(x\right)=3x et v(x)=ln⁡(x)v\left(x\right)=\ln \left(x\right).
Ainsi u′(x)=3u'\left(x\right)=3 et v′(x)=1xv'\left(x\right)=\frac{1}{x}
Ainsi :
F′(x)=−2x+2+3ln⁡(x)+3x×1xF'\left(x\right)=-2x+2+3\ln \left(x\right)+3x\times \frac{1}{x} équivaut successivement à
F′(x)=−2x+2+3ln⁡(x)+3F'\left(x\right)=-2x+2+3\ln \left(x\right)+3
F′(x)=−2x+5+3ln⁡(x)F'\left(x\right)=-2x+5+3\ln \left(x\right)
F′(x)=f(x)F'\left(x\right)=f\left(x\right)

FF est donc une primitive de ffsur [0,5;6]\left[0,5; 6\right].
Question 10

En déduire l'aire exacte, en unités d'aire, du domaine compris entre la courbe (C)\left(C\right), l'axe des abscisses et les droites d'équation x=1x=1 et x=2x=2.
En donner ensuite une valeur arrondie au dixième.

Correction
Soit AA l'aire demandée, ff est positive sur [1;2]\left[1; 2\right] donc
A=∫12f(x)dxA=\int _{{\text 1}}^{2}f\left(x\right)dx équivaut successivement à
A=F(2)−F(1)A=F\left(2\right)-F\left(1\right)
A=−22+2×2+3×2ln⁡(2)−(−12+2×1+3×1ln⁡(1))A=-2^{2} +2\times 2+3\times 2\ln \left(2\right)-\left(-1^{2} +2\times 1+3\times 1\ln \left(1\right)\right)
A=6ln⁡(2)−1A=6\ln (2)-1
A≈3,159u.aA\approx 3,159u.a

L'aire est égale à 6ln⁡(2)−1≈3,26\ln(2)-1\approx 3,2 unités d'aire au dixième près.