La fonction logarithme
Etudes de fonctions - Exercice 1
12 min
20
Question 1
On considère la fonction définie sur l'intervalle par .
On note sa courbe représentative dans un repère du plan.
On note sa courbe représentative dans un repère du plan.
Calculer la dérivée de la fonction .
Correction
est dérivable sur .
On a :
On a :
Question 2
Dresser le tableau de variation de sur .
Correction
D'après la question précédente, nous savons que :
Pour tout réel , on vérifie aisément que . Le signe de dépend alors de .
.
Cela signifie que l'on mettra le signe pour le signe de dès que . On en déduit le tableau de variation suivant :
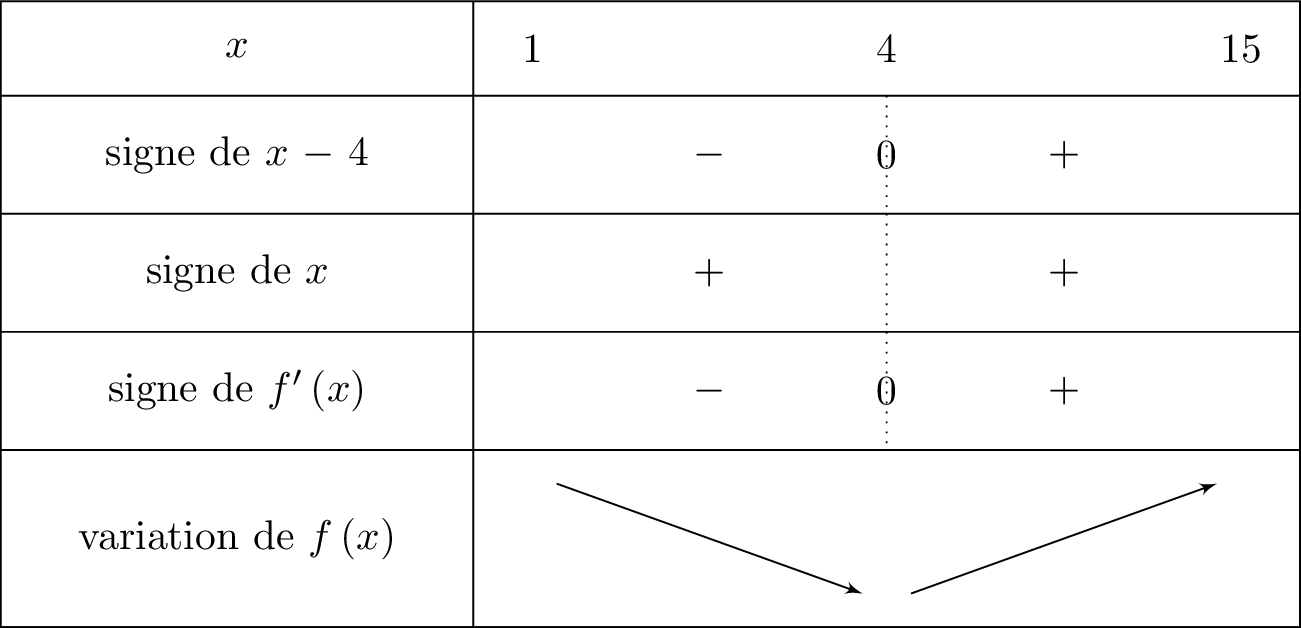
Pour tout réel , on vérifie aisément que . Le signe de dépend alors de .
.
Cela signifie que l'on mettra le signe pour le signe de dès que . On en déduit le tableau de variation suivant :

Question 3
Déterminer une équation de la tangente à la courbe au point d'abscisse .
Correction
L'équation de la tangente au point d'abscisse s'écrit .
Ici , ce qui donne, .1ère étape : calculer
2ème étape : calculer
3ème étape : on remplace les valeurs de et de dans la formule de l'équation de tangente.
On sait que :
Ainsi l'équation de la tangente à la courbe au point d'abscisse est alors :