La fonction logarithme
Domaine de définition pour préparer les équations et inéquations - Exercice 1
15 min
25
Question 1
Correction
La fonction est définie si et seulement si :
Ainsi le domaine de définition est :
Ainsi le domaine de définition est :
Question 2
Correction
La fonction est définie si et seulement si :
Ainsi le domaine de définition est :
Ainsi le domaine de définition est :
Question 3
Correction
La fonction est définie si et seulement si :
Ainsi le domaine de définition est :
Ainsi le domaine de définition est :
Question 4
Correction
La fonction est définie si et seulement si :
autrement dit
On fait l'intersection des deux intervalles.
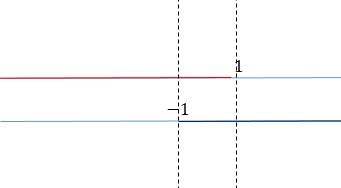
On garde la zone où les deux ensembles sont coloriés simultanément.
Ici c'est la zone entre les deux barres pointillées verticales.
Ainsi le domaine de définition est :
autrement dit
On fait l'intersection des deux intervalles.

On garde la zone où les deux ensembles sont coloriés simultanément.
Ici c'est la zone entre les deux barres pointillées verticales.
Ainsi le domaine de définition est :
Question 5
Correction
La fonction est définie si et seulement si : .
On utilise le discriminant.
~; et .
Comme , la parabole est tournée vers le haut c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
On dresse ensuite le tableau de signe :

Ainsi le domaine de définition est :
On utilise le discriminant.
~; et .
Comme , la parabole est tournée vers le haut c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
On dresse ensuite le tableau de signe :

Ainsi le domaine de définition est :