La fonction exponentielle
Exercices types : ème partie - Exercice 1
45 min
70
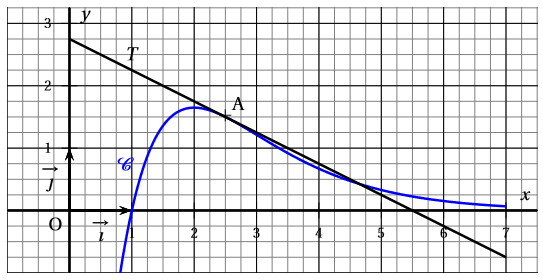
Sur le graphique ci-dessous, est la courbe représentative, dans le repère orthonormé d'une fonction définie sur .

Question 1
Partie A - Étude graphique
La droite est tangente à au point et d’ordonnée à l’origine . L’axe des abscisses est asymptote horizontale à au voisinage de . Déterminer graphiquement :
La droite est tangente à au point et d’ordonnée à l’origine . L’axe des abscisses est asymptote horizontale à au voisinage de . Déterminer graphiquement :
Correction

Question 2
Correction

De plus, le point appartient à cette tangente. Nous allons appelé ce point
A l'aide du point et du point on va pouvoir donner le coefficient directeur de la tangente.
Question 3
Une équation de la tangente .
Correction
Il s'agit ici de l'équation de la tangente au point d'abscisse .
Question 4
Partie B- Modélisation On admet qu’il existe deux réels et tels que , pour tout réel , on a :
Calculer en fonction de et .
Correction
Soit :
Ici on reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
Ici on reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
Question 5
Déduire des questions précédentes un système d’équations vérifiées par et .
Correction
ce qui nous donne ou encore
Or ce qui permet de dire que
équivaut successivement à :
Question 6
Résoudre ce système et en déduire l’expression de en fonction de .
Correction
Il nous faut donc résoudre le système suivant :
équivaut successivement à :
Comme alors
équivaut successivement à :
Comme alors
Question 7
Partie C- Étude algébrique
On admet que pour tout réel ,
On admet que pour tout réel ,
Calculer pour tout réel .
Correction
Ici on reconnaît la forme avec et .
Ainsi et .
Il vient alors que :
Ainsi et .
Il vient alors que :
Question 8
Étudier le signe de et en déduire le tableau des variations de la fonction .
Correction
Pour tout réel , on sait que . Il en résulte donc que le signe de dépend de .
Or :
Il en résulte donc que :
Nous allons donner ci-dessous le tableau de variation complet de .
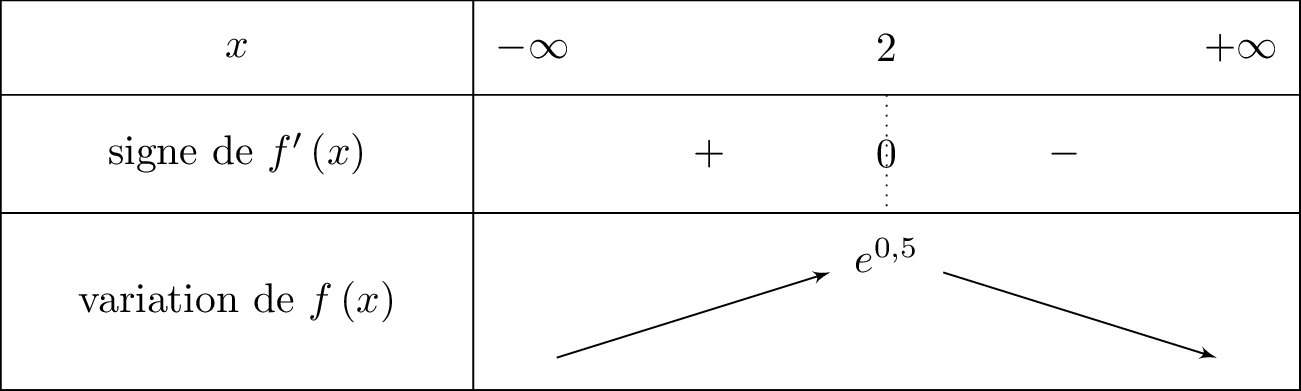
Or :
Il en résulte donc que :
- si alors et donc est croissante sur cet intervalle.
- si alors et donc est décroissante sur cet intervalle.
Nous allons donner ci-dessous le tableau de variation complet de .

Question 9
Vérifier qu’une primitive de la fonction sur est la fonction définie par :
Correction
Dans le cas où une primitive est donnée, il vous suffit de dériver et d'obtenir comme résultat .
Autrement dit, il faut que :
Soit : Autrement dit, il faut que :
On reconnaît la forme : avec et .
Ainsi : et .
Il vient alors que :
Nous avons bien vérifié qu’une primitive de la fonction sur est la fonction définie par :
Question 10
Calculer la valeur exacte de
Correction