La fonction exponentielle
Exercices types : ème partie - Exercice 1
45 min
70
Soit la fonction définie sur par où est un nombre réel.
On admet dans tout l’exercice que la fonction est deux fois dérivable sur l’intervalle . La courbe représentative de la fonction est donnée ci-dessous dans un repère d’origine .
On admet dans tout l’exercice que la fonction est deux fois dérivable sur l’intervalle . La courbe représentative de la fonction est donnée ci-dessous dans un repère d’origine .
Question 1
Les courbes et passent toutes les deux par le point . La droite est tangente à la courbe au point et admet pour équation . On rappelle que désigne la fonction dérivée de la fonction .
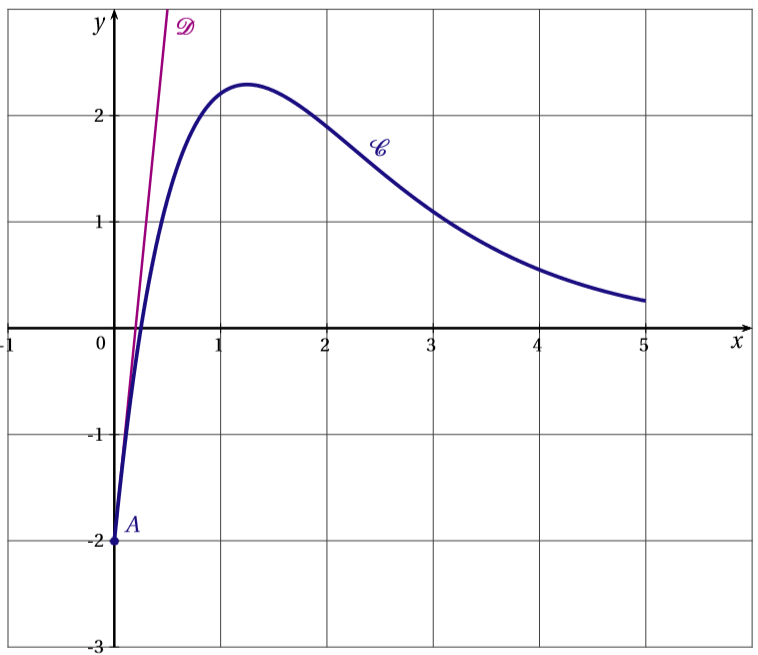

Donner, à l’aide des informations ci-dessus et sans justifier les valeurs de et de .
Correction
D'après le graphique :
Pour déterminer la valeur de , on doit lire le coefficient directeur de la tangente au point d'abscisse . Or, nous savons que la droite est tangente à la courbe au point et admet pour équation donc :
Pour déterminer la valeur de , on doit lire le coefficient directeur de la tangente au point d'abscisse . Or, nous savons que la droite est tangente à la courbe au point et admet pour équation donc :
Question 2
Montrer que pour tout réel appartenant à , on a : .
Correction
Soit :
Ici on reconnaît la forme : avec et .
Ainsi : et .
Il vient alors que :
équivaut successivement à :
. Nous factorisons maintenant par .
Ici on reconnaît la forme : avec et .
Ainsi : et .
Il vient alors que :
équivaut successivement à :
. Nous factorisons maintenant par .
Question 3
Déduire des questions précédentes que .
Correction
Nous savons que : et que . Il en résulte que :
équivaut successivement à :
ainsi :
équivaut successivement à :
ainsi :
Question 4
Donner l'expression de
Correction
Nous savons que : et que . Il en résulte que :
ce qui nous donne :
ce qui nous donne :
Question 5
Etudier le signe de sur l'intervalle . En déduire les variations de sur .
Correction
Pour tout réel appartenant à l'intervalle , on sait que donc le signe de dépend de .
Ainsi :
équivaut successivement à :
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera inférieur ou égale à .
De plus :
; ;
On en déduit le tableau suivant :
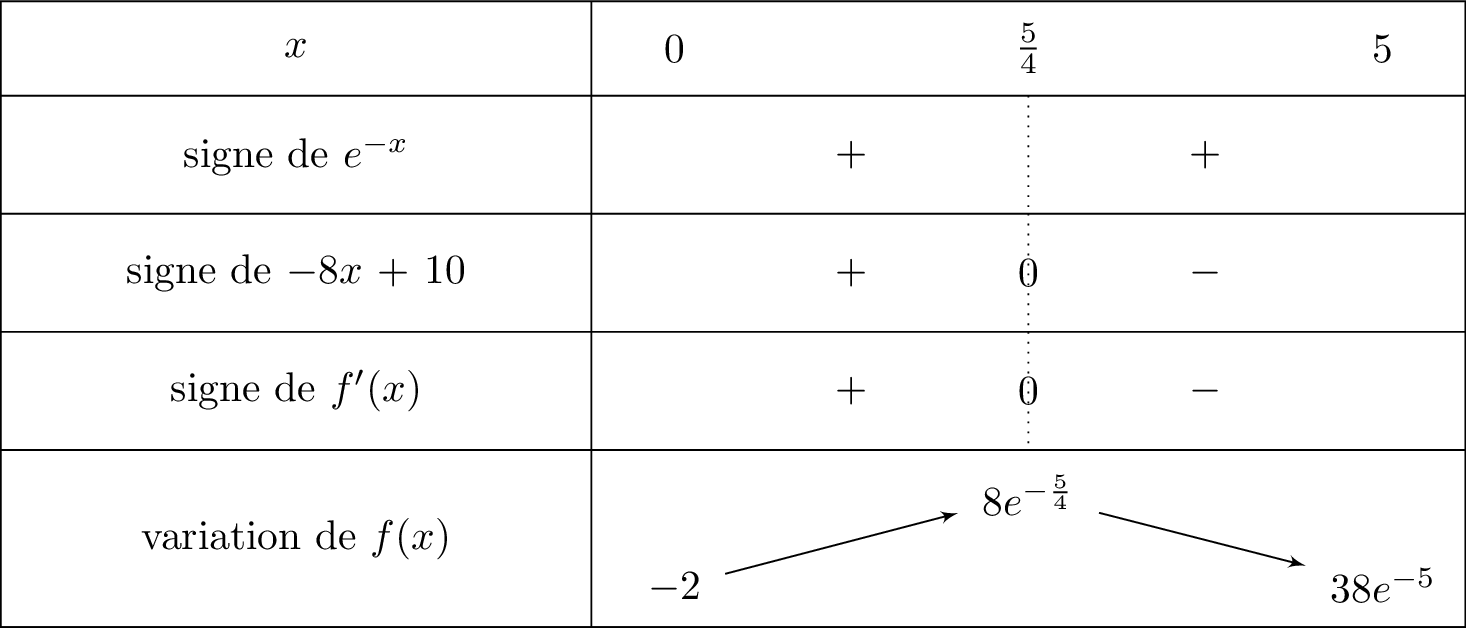
Ainsi :
équivaut successivement à :
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera inférieur ou égale à .
De plus :
; ;
On en déduit le tableau suivant :

Question 6
Résoudre sur l'intervalle l'équation : .
Correction
Nous savons que et . Ainsi :
De plus, pour tout réel appartenant à l'intervalle , on sait que : .
Ainsi :
équivaut successivement à :
ou
Or une exponentielle est positive donc l'équation n'a pas de solution.
D'où : ainsi
La solution de l'équation est :
De plus, pour tout réel appartenant à l'intervalle , on sait que : .
Ainsi :
équivaut successivement à :
ou
Or une exponentielle est positive donc l'équation n'a pas de solution.
D'où : ainsi
La solution de l'équation est :
Question 7
À l’aide d’un logiciel de calcul formel, on a obtenu les résultats suivants :
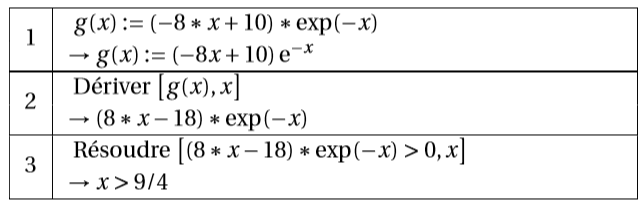
En utilisant ces résultats :
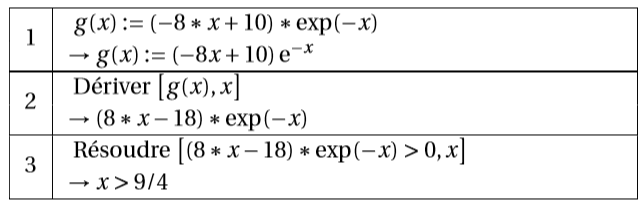
En utilisant ces résultats :
Donner l’expression de , fonction dérivée seconde de la fonction .
Correction
La première ligne sert uniquement à rentrer la définition de la fonction .
La deuxième ligne permet donc de calculer .
Il en résulte donc que :
La deuxième ligne permet donc de calculer .
Il en résulte donc que :
Question 8
Justifier que la courbe admet un point d’inflexion dont on donnera la valeur exacte de l’abscisse.
Correction
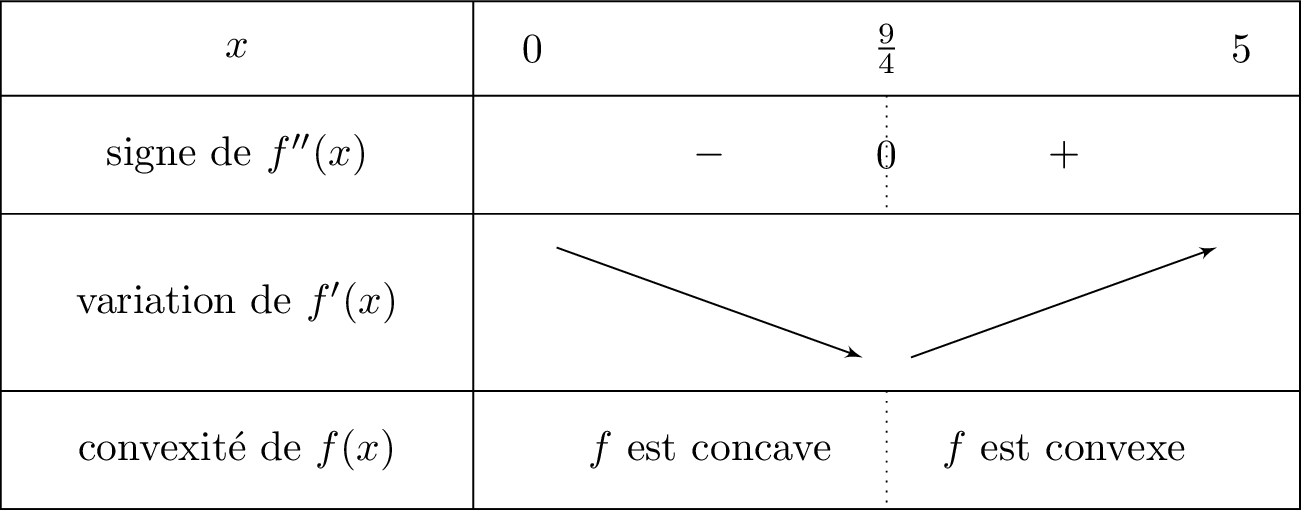
- possède un point d'inflexion lorsque sa dérivée seconde s'annule et change de signe en ce point.
Pour tout réel appartenant à l'intervalle , on sait que , donc le signe de dépend alors de .
équivaut successivement à :
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera supérieur ou égale à .
possède bien un point d'inflexion au point d'abscisse car sa dérivée seconde s'annule et change de signe en ce point; comme le justifie le tableau de signe suivant :
Question 9
Une entreprise fabrique des grille-pains. Après avoir fait une étude, son directeur constate que si l’entreprise fabrique chaque jour milliers de grille pains (où est un nombre réel de l’intervalle ), alors le bénéfice quotidien est donné, en centaine de milliers d’euros, par la fonction définie par :
Quelle quantité de grille-pains l’entreprise doit-elle fabriquer afin de réaliser un bénéfice maximal?
Correction
D’après le tableau des variations, la fonction admet un maximum pour . Le bénéfice sera donc maximum pour grille-pains.
Question 10
Quel est alors la valeur de ce bénéfice maximal? On donnera une valeur approchée du résultat à l’euro près.
Correction
Nous savons que
Le bénéfice maximum sera donc de euros.
Le bénéfice maximum sera donc de euros.