La fonction exponentielle
Exercice 2 - Exercice 1
1 min
0
Dans un laboratoire, des scientifiques ont étudié pendant ans l'effet de la pollution sur une population d'insectes car ils craignaient l'extinction de cette espèce.
L'étude a été effectuée sur un échantillon de insectes.
Les deux parties peuvent être traitées indépendamment l'une de l'autre.
L'étude a été effectuée sur un échantillon de insectes.
Les deux parties peuvent être traitées indépendamment l'une de l'autre.
Question 1
Partie A
Une étude a permis de montrer que la population d'insectes diminue très rapidement lors des quatre premières années.
La population peut être modélisée par la fonction définie sur l'intervalle par :
, où est le temps exprimé en années et le nombre de milliers d'insectes.
Une étude a permis de montrer que la population d'insectes diminue très rapidement lors des quatre premières années.
La population peut être modélisée par la fonction définie sur l'intervalle par :
, où est le temps exprimé en années et le nombre de milliers d'insectes.
Calculer le pourcentage de diminution du nombre d'insectes la première année.
Arrondir à .
Arrondir à .
Correction
Le nombre de milliers d'insectes est donné par où est exprimé en années, donc le nombre d'insectes au départ est , et le nombre d'insectes au bout d'un an est .
Le pourcentage d'évolution est :
Le pourcentage de diminution du nombre d'insectes la première année est approximativement de .
Le pourcentage d'évolution est :
Le pourcentage de diminution du nombre d'insectes la première année est approximativement de .
Question 2
Montrer que la fonction définie sur l'intervalle par est une primitive de la fonction sur l'intervalle .
Correction
Dans le cas où une primitive est donnée, il vous suffit de dériver et d'obtenir comme résultat .
Autrement dit, il faut que :
La fonction définie sur , par est une primitive de si, pour tout de , .Autrement dit, il faut que :
Ainsi :
Donc est une primitive de sur .
Question 3
Calculer la valeur exacte de .
Correction
On commence donc à déterminer une primitive de .
D'après la question ,
Il vient alors :
D'après la question ,
Il vient alors :
Question 4
En déduire la population moyenne d'insectes entre le début de la deuxième et le début de la quatrième année.
Correction
On calcule la valeur moyenne de la fonction entre et
Ensuite, on applique la formule de la valeur moyenne :
équivaut successivement à
Soit u ne fonction continue sur un intervalle . La valeur moyenne de la fonction sur est le réel défini par :
Ensuite, on applique la formule de la valeur moyenne :
équivaut successivement à
Question 5
Partie B
Après de longues recherches, un biologiste a mis au point un traitement pour essayer de sauver cette espèce.
Ce traitement est administré aux insectes à partir de la quatrième année.
L'évolution de la population est alors modélisée par la fonction définie sur l'intervalle par :
Après de longues recherches, un biologiste a mis au point un traitement pour essayer de sauver cette espèce.
Ce traitement est administré aux insectes à partir de la quatrième année.
L'évolution de la population est alors modélisée par la fonction définie sur l'intervalle par :
On désigne par la fonction dérivée de la fonction .
Montrer que pour tout réel de l'intervalle , .
Montrer que pour tout réel de l'intervalle , .
Correction
On reconnait la forme
Comme alors :
Comme alors :
Question 6
On admet que la fonction est continue et strictement croissante sur l'intervalle .
Montrer que l'équation a une solution et une seule dans l'intervalle .
Donner la valeur arrondie au dixième de .
Montrer que l'équation a une solution et une seule dans l'intervalle .
Donner la valeur arrondie au dixième de .
Correction
On admet que la fonction est continue et strictement croissante sur l'intervalle .
et
On établit le tableau de variation de la fonction sur l'intervalle
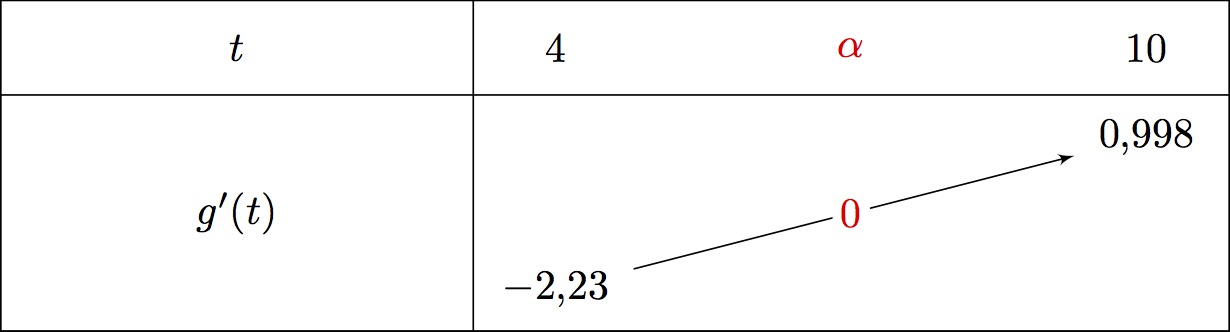
D'après le tableau de variation de on peut déduire que l'équation admet une solution unique dans l'intervalle .
Donc la valeur arrondie au dixième de est .
et
On établit le tableau de variation de la fonction sur l'intervalle

D'après le tableau de variation de on peut déduire que l'équation admet une solution unique dans l'intervalle .
Donc la valeur arrondie au dixième de est .
Question 7
En déduire le signe de sur l'intervalle .
Correction
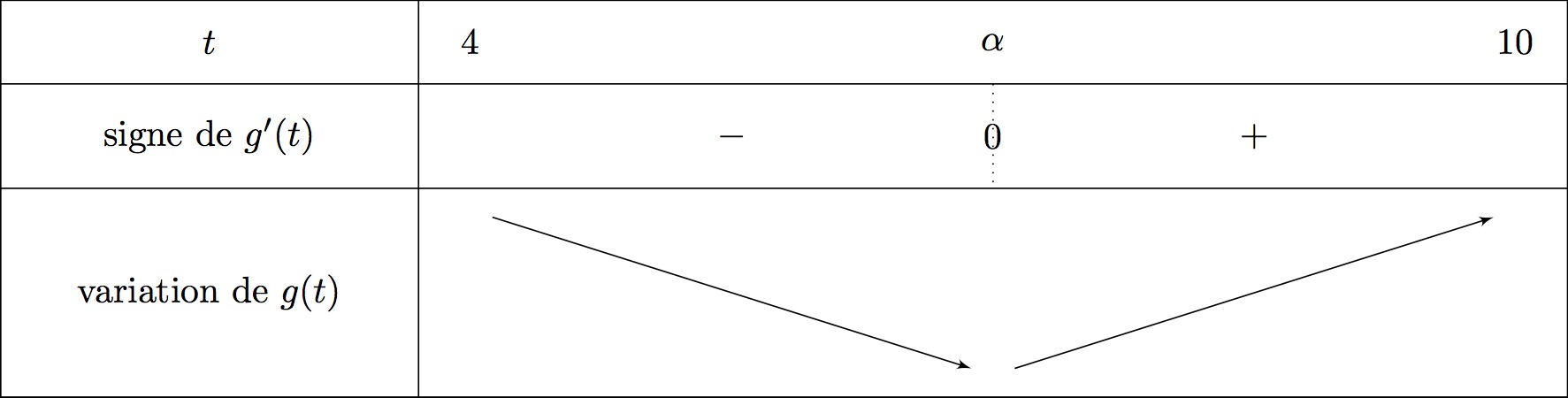
D'après le tableau de variation de la fonction sur , on peut dire que :
- sur
- et
- sur
Question 8
Donner le sens de variation de la fonction sur l'intervalle .
Correction
- La fonction est strictement décroissante sur
- La fonction est strictement croissante sur .
Question 9
Que peut-on supposer quant à l'effet du traitement sur la population d'insectes ?
Correction
D'après les résultats des questions précédentes, on peut voir que le nombre d'insectes commence à remonter à partir de , c'est-à-dire à partir de la sixième année puisque .
Donc le traitement semble efficace sur la population d'insectes à partir de la sixième année.
Donc le traitement semble efficace sur la population d'insectes à partir de la sixième année.