Echantillonnage et estimation
Exercice 7 - Exercice 1
1 min
0
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse en justifiant la réponse.
Question 1
On considère l’arbre de probabilité ci-contre :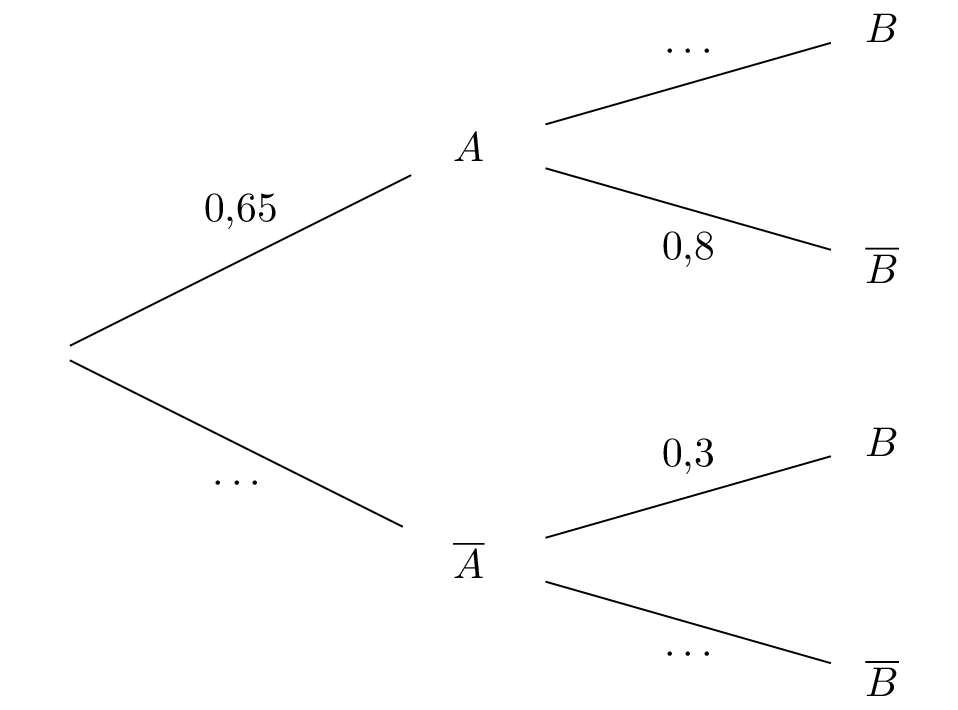

Affirmation : La probabilité de est égale à .
Correction
Dans un premier temps, nous allons compléter l'arbre de probabilité.
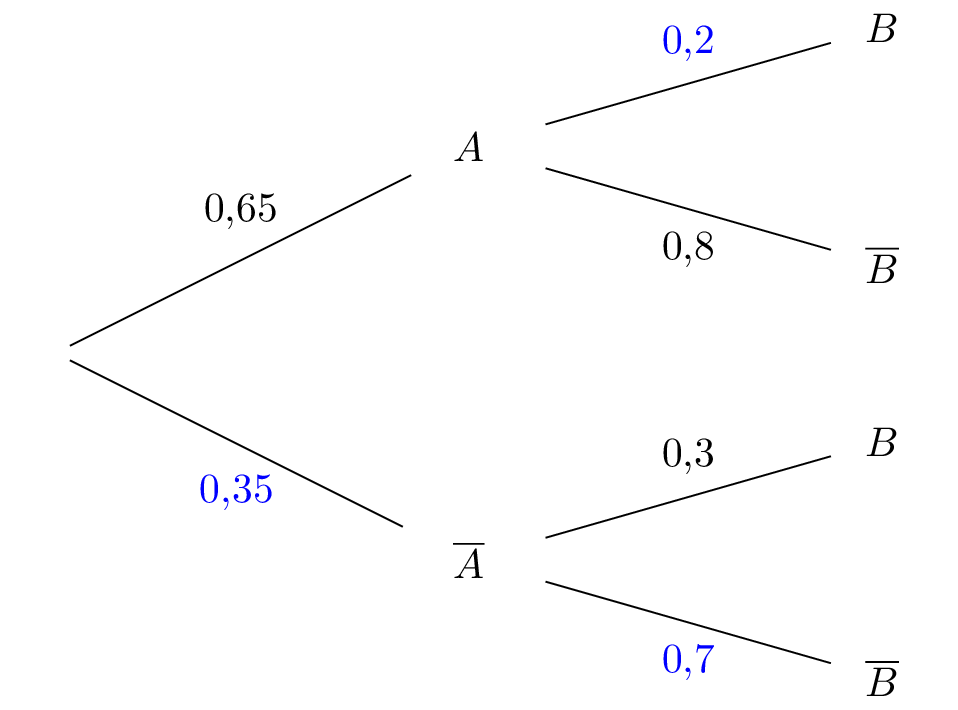
D'après la formule des probabilités totales on a :
Soit :
Ainsi :
Question 2
Affirmation :
Correction

car d'après la question précédente, nous savons que :
arrondi à près.
Question 3
Un institut de sondage affirme que des Français écoutent de la musique classique, au moins de temps en temps. On interroge Français, et parmi eux déclarent écouter de la musique classique de temps en temps.
Affirmation : On peut rejeter, avec un risque d’erreur inférieur à , le résultat donné par l’institut de sondage.
Correction
Il faut vérifier les conditions suivantes , et .
Ici et
- donc
- donc
- donc
On a alors :
Ici est une valeur approchée par défaut de
Ici est une valeur approchée par excès de
Nous allons déterminer maintenant la fréquence des personnes déclarant écouter de la musique classique de temps en temps dans l'échantillon. Il vient que :
Or , donc la fréquence ddes personnes déclarant écouter de la musique classique de temps en temps dans l'échantillon n'est pas dans l'intervalle.
On peut rejeter, avec un risque d’erreur inférieur à , le résultat donné par l’institut de sondage.
Question 4
La courbe de densité d’une variable aléatoire suivant la loi normale d’espérance et d’écart-type est donnée ci-dessous. La valeur de l’aire de la surface grisée est de . 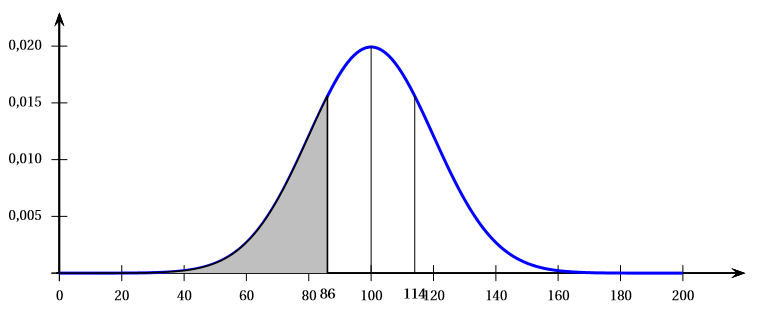

Affirmation : La probabilité que soit comprise entre et est égale à .
Correction
Nous remarquons que et de ce fait
- Soit un réel positif et une loi normale suivant les paramètres et alors :
De plus, nous savons que l'aire sous la cloche est égale à .
Donc :