Echantillonnage et estimation

Exercice 3 - Exercice 1

1 min
0
Le service marketing d'un magasin de téléphonie a procédé à une étude du comportement de sa clientèle.
Il a ainsi observé que celle-ci est composée de 42%42\% de femmes, 35%35\% des femmes qui entrent dans le magasin y effectuent un achat, alors que cette proportion est de 55%55\% pour les hommes.
Une personne entre dans le magasin.
On note :
  • FF l'évènement : « La personne est une femme »
  • RR l'évènement : « La personne repart sans rien acheter »
Dans tout l'exercice, donner des valeurs approchées des résultats au millième.
Les parties AA, BB et CC peuvent être traitées de manière indépendante.
Question 1
Partie A.

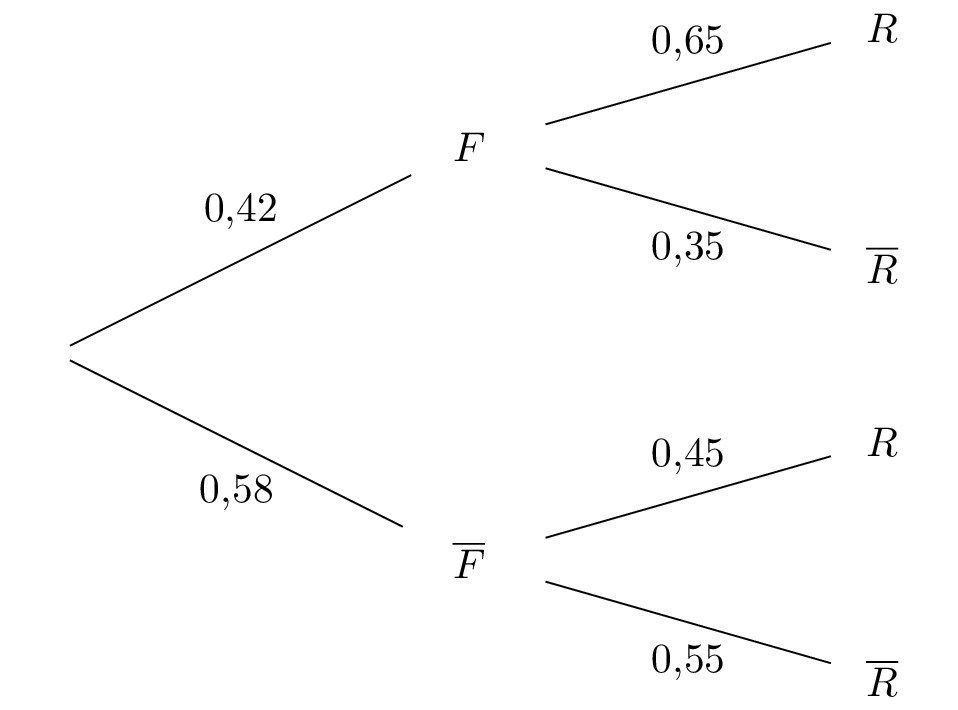
Construire un arbre pondéré illustrant la situation.

Correction
L'arbre pondéré illustrant la situation est le suivant :
Question 2

Calculer la probabilité que la personne qui est entrée dans le magasin soit une femme et qu'elle reparte sans rien acheter.

Correction
On calcule
P(F∩R)=P(F)×PF(R)P(F\cap R)=P(F)\times P_{F} (R)
P(F∩R)=0,42×0,65P(F\cap R)=0,42\times 0,65
P(F∩R)=0,273P(F\cap R)=0,273
Question 3

Montrer que P(R)=0,534P(R)=0,534.

Correction
Les évènements FF et F‾\overline{F} forment une partition de l'univers.
D'après la formule des probabilités totales on a :
P(R)=P(F∩R)+P(F‾∩R)P(R)=P(F\cap R)+P(\overline{F}\cap R)
P(R)=P(F)×PF(R)+P(F‾)×PF‾(R)P(R)=P(F)\times P_{F} (R)+P(\overline{F})\times P_{\overline{F}} (R)
P(R)=0,42×0,65+0,58×0,45P(R)=0,42\times 0,65+0,58\times 0,45
P(R)=0,534P(R)=0,534
Question 4
Partie B
Un client du magasin s'inquiète de la durée de vie du téléphone de type T1 qu'il vient de s'offrir.
On note XX la variable aléatoire qui, à chaque téléphone mobile de type T1 prélevé au hasard dans la production, associe sa durée de vie, en mois.
On admet que la variable aléatoire XX suit la loi normale d'espérance μ=48\mu =48 et d'écart-type σ=10\sigma =10.

Justifier que la probabilité que le téléphone de type T1 prélevé fonctionne plus de 33 ans, c'est-à-dire 3636 mois, est d'environ 0,8850,885.

Correction
Il faut calculer ici P(X≥36)P\left(X\ge 36\right)
Pour le calcul de P(X≥36)P\left(X\ge 36\right)
Avec une Texas, on tape pour P(X≥36)P\left(X\ge 36\right) NormalFrep(valeur min,valeur max ,espérance , écart type ) c'est-à-dire ici NormalFrep(3636 , 109910^{99} , 48 48 , 1010 ) puis taper sur enter et vous obtiendrez :
P(X≥36)≈0,885P\left(X\ge 36\right)\approx 0,885

Avec une Casio Graph 35+, on tape pour P(X≥36)P\left(X\ge 36\right)
Normal C.D
Lower : 3636 Valeur Minimale
Upper : 109910^{99} Valeur Maximale
σ\sigma : 1010 Ecart type
μ\mu : 4848 Espérance

puis taper sur EXE et vous obtiendrez :
P(X≥36)≈0,885P\left(X\ge 36\right)\approx 0,885
Question 5

On sait que le téléphone de type T1 prélevé a fonctionné plus de 33 ans.
Quelle est la probabilité qu'il fonctionne moins de 55 ans ?

Correction
Il s'agit d'une probabilité conditionnelle.
Il vient alors que :
PX≥36(X≤60)=P((X≥36)∩(X≤60))P(X≥36)P_{X\ge 36} \left(X\le 60\right)=\frac{P\left(\left(X\ge 36\right)\cap \left(X\le 60\right)\right)}{P\left(X\ge 36\right)}
PX≥36(X≤60)=P(36≤X≤60)P(X≥36)P_{X\ge 36} \left(X\le 60\right)=\frac{P\left(36\le X\le 60\right)}{P\left(X\ge 36\right)} . On calcule P(36≤X≤60)≈0,76986P\left(36\le X\le 60\right)\approx 0,76986
PX≥36(X≤60)=0,769860,884930P_{X\ge 36} \left(X\le 60\right)=\frac{0,76986}{0,884930}
PX≥36(X≤60)=0,870P_{X\ge 36} \left(X\le 60\right)=0,870
Question 6
Partie C
Le gérant du magasin émet l'hypothèse que 30%30\% des personnes venant au magasin achètent uniquement des accessoires (housse, chargeur, ... ).
Afin de vérifier son hypothèse, le service marketing complète son étude.

Déterminer l'intervalle de fluctuation asymptotique au seuil de 95%95\% de la fréquence de personnes ayant uniquement acheté des accessoires dans un échantillon de taille 15001 500.

Correction
D'après l'énoncé, on a p=0,3p=0,3 et n=1500n=1500.
Il faut vérifier les conditions suivantes n≥30n\ge 30 , np≥5np\ge 5 et n(1−p)≥5n\left(1-p\right)\ge 5.
  • 1500≥301500\ge 30 donc n≥30n\ge 30
  • 1500×0,3=4501500\times 0,3=450 donc np≥5np\ge 5
  • 1500×(1−0,3)=10501500\times \left(1-0,3\right)=1050 donc n(1−p)≥5n\left(1-p\right)\ge 5

Les trois conditions sont réalisées, on peut donc calculer l'intervalle de fluctuation asymptotique au seuil de 95%.
On a alors :
I=[p−1,96×p×(1−p)n;p+1,96×p×(1−p)n]I=\left[p-1,96\times \frac{\sqrt{p\times \left(1-p\right)} }{\sqrt{n} } ;p+1,96\times \frac{\sqrt{p\times \left(1-p\right)} }{\sqrt{n} } \right]
I=[0,3−1,96×0,3×(1−0,3)1500;0,3+1,96×0,3×(1−0,3)1500]I=\left[0,3-1,96\times \frac{\sqrt{0,3\times \left(1-0,3\right)} }{\sqrt{1500} } ;0,3+1,96\times \frac{\sqrt{0,3\times \left(1-0,3\right)} }{\sqrt{1500} } \right]
I=[0,276;0,323]I=\left[0,276;0,323\right]
Ici 0,2760,276 est une valeur approchée par défaut de 0,3−1,96×0,3×(1−0,3)15000,3-1,96\times \frac{\sqrt{0,3\times \left(1-0,3\right)} }{\sqrt{1500} }
Ici 0,3230,323 est une valeur approchée par excès de 0,3+1,96×0,3×(1−0,3)15000,3+1,96\times \frac{\sqrt{0,3\times \left(1-0,3\right)} }{\sqrt{1500} }
Question 7

Le service marketing interroge un échantillon de 15001500 personnes.
L'étude indique que 430430 personnes ont acheté uniquement des accessoires.
Doit-on rejeter au seuil de 5%5\% l'hypothèse formulée par le gérant ?

Correction
La fréquence observée pour l'échantillon vaut fobs=4301500≈0,287f_{obs} =\frac{430}{1500} \approx 0,287
Or fobs∈[0,276;0,323]f_{obs} \in \left[0,276;0,323\right]
Il en résulte que l'on peut accepter l'hypothèse de p=0,3p=0,3 au seuil de 95%95\%.