Continuité, dérivation, lectures graphiques et convexité
Exercices types : ème partie. Applications à l'économie - Exercice 1
25 min
40
Une entreprise lance sur le marché une nouvelle calculatrice mode examen pour le BAC. La production est comprise entre et .
Question 1
Le bénéfice en milliers d'euros pour centaines de calculatrices et vendues est donnée par : avec .
Déterminer le tableau de variation de la fonction sur .
Correction
est dérivable sur .
On a :
Il s'agit d'une équation du second degré. Nous allons utiliser le discriminant.
Nous donnons directement les résultats car le discriminant n'a maintenant plus de secret pour nous.
, et
Comme , la parabole est tournée vers le bas c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
Cela nous donne ci-dessous :
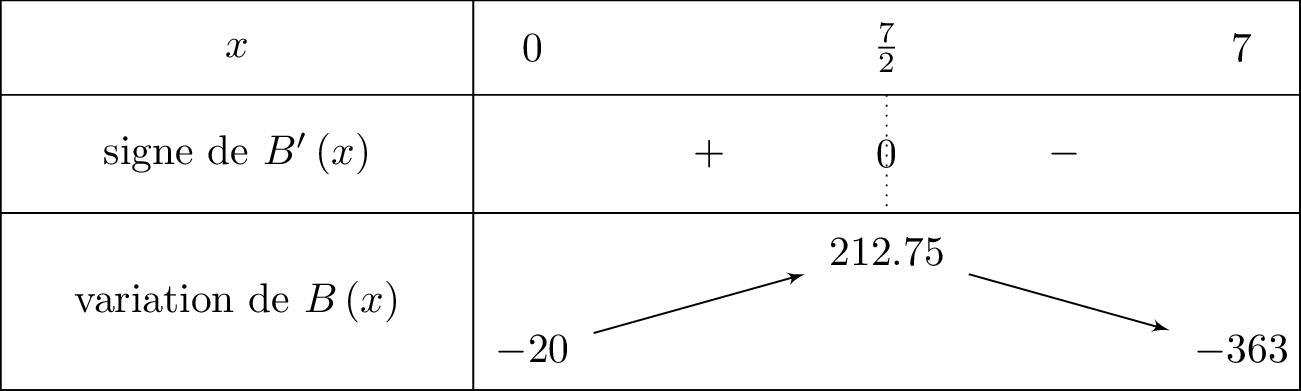 d'où :
d'où :
d'où :
d'où :
On a :
. Il nous faut maintenant étudier le signe de .
Il s'agit d'une équation du second degré. Nous allons utiliser le discriminant.
Nous donnons directement les résultats car le discriminant n'a maintenant plus de secret pour nous.
, et
Comme , la parabole est tournée vers le bas c'est-à-dire que est du signe de à l'extérieur des racines et du signe opposé à entre les racines.
Cela nous donne ci-dessous :

d'où :
d'où :
Question 2
Déterminer le nombre de solutions de l'équation sur .
Correction
Nous allons intégrer dans le tableau les solutions à l'équation . Nous les noterons et .
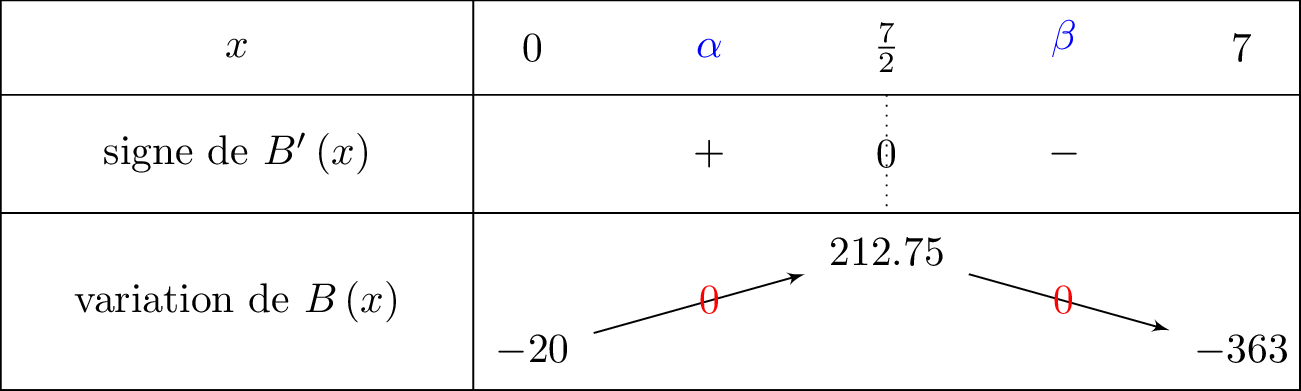 L'équation admet donc deux solutions et sur l'intervalle .
L'équation admet donc deux solutions et sur l'intervalle .

Question 3
Déterminer une valeur approchée de chacune des solutions de l'équation à près.
Correction
A la calculatrice, on vérifie que :
D'une part :
et .
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
D'autre part :
et .
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
D'une part :
et .
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
D'autre part :
et .
Or , donc d'après le théorème des valeurs intermédiaires on en déduit que :
Question 4
En déduire le tableau de signes de sur .
Correction


Question 5
Pour quelles quantités de calculatrices fabriquées et vendues l'entreprise réalise t-elle un bénéfice?
Correction
Il nous faut donner l'intervalle sur lequel . D'après la question , nous pouvons indiquer l'intervalle .
