Continuité, dérivation, lectures graphiques et convexité

Exercice 6 - Exercice 1

1 min
0
La courbe (C)\left(C\right) d'une fonction ff définie et dérivable sur R\mathbb{R} est donnée ci-dessous.
La courbe (C)\left(C\right) passe par les points A(−1;e)A\left(-1;e\right) et B(0;2)B\left(0;2\right).
La tangente à la courbe (C)\left(C\right) au point AA est horizontale et la tangente à la courbe (C)\left(C\right) au point BB est la droite (BD)\left(BD\right), où DD a pour coordonnées (2;0)\left(2;0\right).
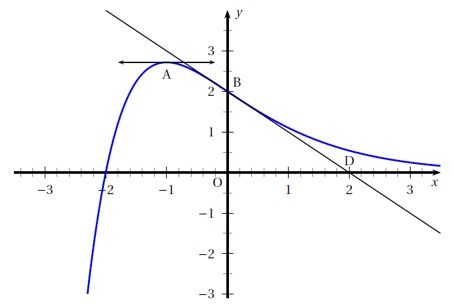Pour chacune des affirmations suivantes, indiquer, en justifiant, si elle est vraie ou fausse en vous appuyant sur la représentation graphique ci-dessus.
Question 1

L'équation f(x)=1f\left(x\right)=1 admet exactement trois solutions dans l'intervalle [−2;3]\left[-2;3\right].
  • Vrai
  • Faux

Correction
La proposition est fausse.
L'équation f(x)=1f\left(x\right)=1 admet exactement deux solutions dans l'intervalle [−2;3]\left[-2;3\right].
Il suffit de tracer la droite d'équation y=1y=1 et celle-ci coupe la courbe deux fois.
Question 2

La fonction ff est convexe sur l'intervalle [1;3]\left[1;3\right].
  • Vrai
  • Faux

Correction
La proposition est vraie.
  • ff est convexe sur [a;b]\left[a;b\right] si et seulement si sa courbe est entièrement située au-dessus de chacune de ses tangentes.
  • ff est concave sur [a;b]\left[a;b\right] si et seulement si sa courbe est entièrement située en dessous de chacune de ses tangentes.
Sur l'intervalle [1;3]\left[1;3\right], la courbe (C)\left(C\right) est entièrement située au-dessus de chacune de ses tangentes.
Question 3

f′(1)=0f'\left(1\right)=0
  • Vrai
  • Faux

Correction
La proposition est vraie.
La tangente à la courbe au point AA d'abscisse −1-1 est horizontale.
Question 4

f′(0)=−1f'\left(0\right)=-1
  • Vrai
  • Faux

Correction
La proposition est vraie.
La tangente à la courbe au point d'abscisse 0 est la droite (BD)\left(BD\right).
On va déterminer le coefficient directeur de la droite (BD)\left(BD\right) qui sera égale à f′(0)f'\left(0\right).
Ainsi :
f′(0)=yD−yBxD−xBf'\left(0\right)=\frac{y_{D} -y_{B} }{x_{D} -x_{B} }
f′(0)=0−22−0f'\left(0\right) =\frac{0-2}{2-0}
donc
f′(0)=−1f'\left(0\right)=-1
Question 5

f′(x)≥0f'\left(x\right)\ge 0 sur l'intervalle [1;3]\left[1;3\right].
  • Vrai
  • Faux

Correction
La proposition est fausse.
  • Si ff est décroissante sur [a;b]\left[a;b\right] alors f′f' est négative sur [a;b]\left[a;b\right]
  • Si ff est croissante sur [a;b]\left[a;b\right] alors f′f' est positive sur [a;b]\left[a;b\right]
La fonction ff est décroissante sur cet intervalle donc sa dérivée est négative.
Question 6

Une primitive FF de la fonction ff est croissante sur l'intervalle [1;3]\left[1;3\right].
  • Vrai
  • Faux

Correction
La proposition est fausse.
  • Si ff est négative sur [a;b]\left[a;b\right] donc que FF est décroissante sur [a;b]\left[a;b\right].
  • Si ff est positive sur [a;b]\left[a;b\right] donc que FF est croissante sur [a;b]\left[a;b\right].
On peut le démontrer en utilisant le fait que la fonction ff est positive sur l'intervalle [1;3]\left[1;3\right].