Continuité, dérivation, lectures graphiques et convexité
Exercice 5 - Exercice 1
1 min
0
L'exercice suivant est un Q. C. M. (questionnaire à choix multiples).
Pour chaque proposition choisir l'unique bonne réponse.
Vous devez bien sûr justifier.
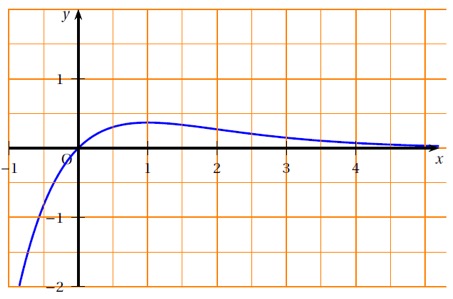
On considère la fonction définie sur par :
La courbe représentative de est tracée dans le repère ci-dessous :
Pour chaque proposition choisir l'unique bonne réponse.
Vous devez bien sûr justifier.
On considère la fonction définie sur par :
La courbe représentative de est tracée dans le repère ci-dessous :

Question 1
Pour tout réel , est égale à :
Correction
La bonne réponse est c.
On reconnait la forme avec et .
Ainsi et .
Donc : .
On factorise par .
On obtient :
Soit .
On reconnait la forme avec et .
Ainsi et .
Donc : .
On factorise par .
On obtient :
Question 2
La tangente à la courbe représentative de au point d'abscisse 0 a pour équation :
Correction
La bonne réponse est a.
On sait que la formule de l'équation de la tangente au point d'abscisse 0 est :
Il en résulte que :
s'écrit :
Ainsi :
On sait que la formule de l'équation de la tangente au point d'abscisse 0 est :
- D'une part : alors
- D'autre part : alors
Il en résulte que :
s'écrit :
Ainsi :
Question 3
Une primitive de est définie sur par :
Correction
La bonne réponse est b.
Une primitive de vérifie
Avec .
On reconnait la forme avec et .
Ainsi et
On obtient :
D'où :
Une primitive de vérifie
Avec .
On reconnait la forme avec et .
Ainsi et
On obtient :
D'où :
Question 4
La valeur de est :
- négative
- inférieure à
- supérieure à
- négative
- inférieure à
- supérieure à
Correction
La bonne réponse est b.
D'après la question précédente, on sait qu'une primitive de s'écrit
Il vient alors que :
D'après la question précédente, on sait qu'une primitive de s'écrit
Il vient alors que :
Question 5
La fonction est :
- concave sur
- convexe sur
- concave sur et convexe sur
- concave sur
- convexe sur
- concave sur et convexe sur
Correction
La bonne réponse est c.
On va étudier le signe de la dérivée seconde de que l'on note
On sait que :
.
On reconnait la forme avec et .
Ainsi et
D'où :
Pour tout réel , on sait que .
Ainsi le signe de la dérivée seconde dépend de .
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera supérieur ou égale à .
On en déduit le tableau de variation suivant :
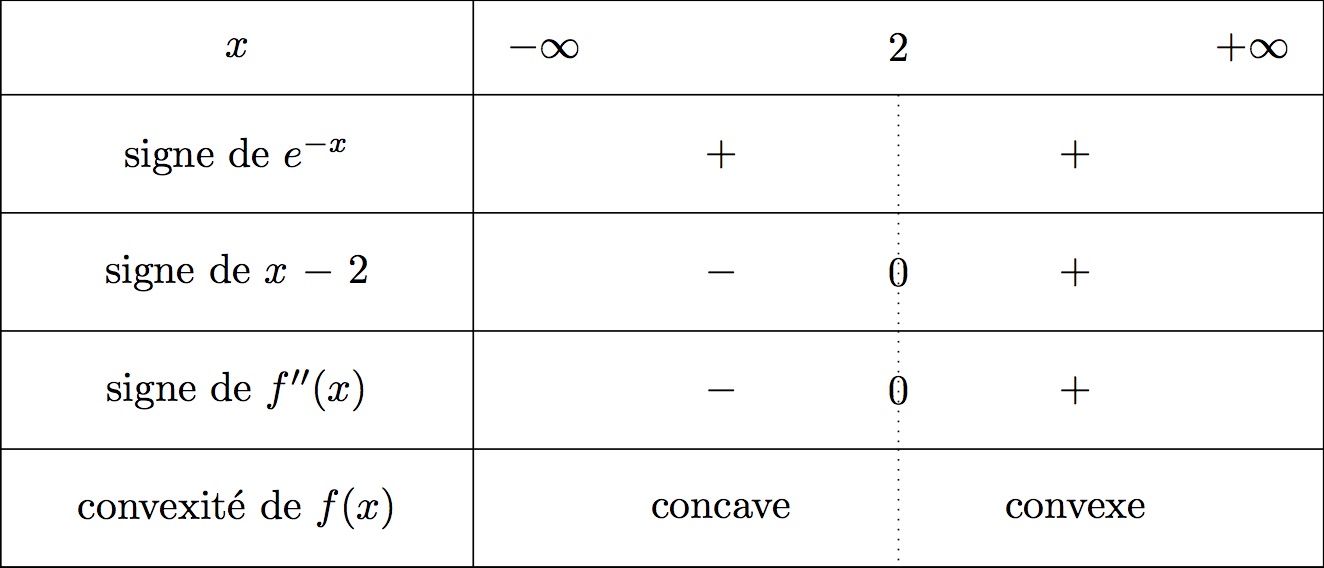
On va étudier le signe de la dérivée seconde de que l'on note
On sait que :
.
On reconnait la forme avec et .
Ainsi et
D'où :
Pour tout réel , on sait que .
Ainsi le signe de la dérivée seconde dépend de .
Cela signifie que l'on va mettre le signe dans la ligne de lorsque sera supérieur ou égale à .
On en déduit le tableau de variation suivant :

Question 6
L'équation admet :
- aucune solution
- une solution
- deux solutions
- aucune solution
- une solution
- deux solutions
Correction
La bonne réponse est a.
A l'aide du graphique, on vérifie facilement que la courbe ne croise pas la droite d'équation .
Il n'a donc pas de solution à l'équation .
A l'aide du graphique, on vérifie facilement que la courbe ne croise pas la droite d'équation .
Il n'a donc pas de solution à l'équation .