Continuité, dérivation, lectures graphiques et convexité
Exercice 4 - Exercice 1
1 min
0
Cet exercice est un questionnaire à choix multiples.
Pour chaque question posée, une seule des réponses proposées est exacte.
On demande bien sûr de justifier.
Dans le plan muni d'un repère orthogonal, on a tracé la courbe représentative d'une fonction définie et dérivable sur ainsi que les tangentes à la courbe aux points , et .
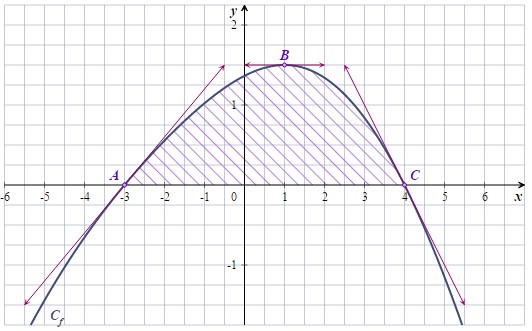
Pour chaque question posée, une seule des réponses proposées est exacte.
On demande bien sûr de justifier.
Dans le plan muni d'un repère orthogonal, on a tracé la courbe représentative d'une fonction définie et dérivable sur ainsi que les tangentes à la courbe aux points , et .

Question 1
On note la dérivée de la fonction alors :
-
-
-
-
Correction
La bonne réponse est d.
correspond au coefficient directeur de la tangente à la courbe au point d'abscisse donc au point .
De plus, le point appartient à cette tangente.
A l'aide du point et du point on va pouvoir donner le coefficient directeur de la tangente.
donc
correspond au coefficient directeur de la tangente à la courbe au point d'abscisse 4 donc au point .
De plus, le point appartient à cette tangente.
A l'aide du point et du point on va pouvoir donner le coefficient directeur de la tangente.
D'où :
correspond au coefficient directeur de la tangente à la courbe au point d'abscisse donc au point .
De plus, le point appartient à cette tangente.
A l'aide du point et du point on va pouvoir donner le coefficient directeur de la tangente.
donc
correspond au coefficient directeur de la tangente à la courbe au point d'abscisse 4 donc au point .
De plus, le point appartient à cette tangente.
A l'aide du point et du point on va pouvoir donner le coefficient directeur de la tangente.
D'où :
Question 2
On note la primitive de la fonction telle que
-
-
-
-
Correction
La bonne réponse est c.
Nous connaissons la représentation graphique de .
Nous allons dresser le tableau de signe de et nous obtiendrons les variations de car on rappelle que
On remarque grâce au graphique de que :
Ce qui donne :
 On sait que et que est croissante sur , il en résulte que .
On sait que et que est croissante sur , il en résulte que .
Nous connaissons la représentation graphique de .
Nous allons dresser le tableau de signe de et nous obtiendrons les variations de car on rappelle que
On remarque grâce au graphique de que :
- est négative sur et sur l'intervalle donc est décroissante sur et sur l'intervalle .
- est positive sur donc que est croissante sur .
Ce qui donne :

Question 3
La fonction est :
- Est concave sur
- Est convexe sur
- Change de convexité pour et
- Change de convexité pour
- Est concave sur
- Est convexe sur
- Change de convexité pour et
- Change de convexité pour
Correction
La bonne réponse est d.
On rappelle que , donc si l'on connait les variations de nous connaitrons le signe de et on déterminera la convexité de .
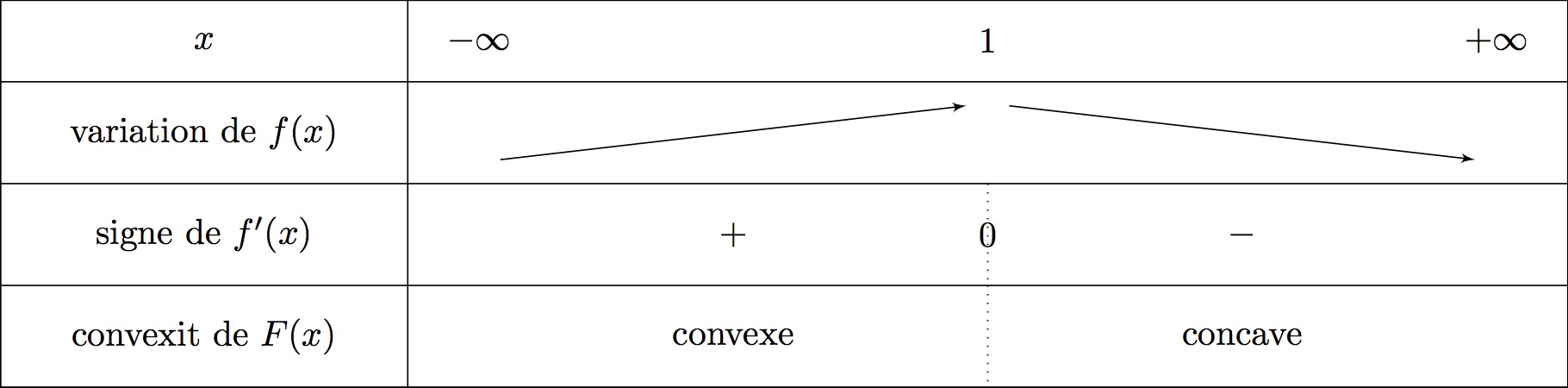 On voit bien que l'unique point d'inflexion est atteint au point d'abscisse .
On voit bien que l'unique point d'inflexion est atteint au point d'abscisse .
On rappelle que , donc si l'on connait les variations de nous connaitrons le signe de et on déterminera la convexité de .

Question 4
On note l'aire, exprimée en unité d'aire, du domaine hachuré :
-
-
-
-
Correction
La bonne réponse est b.
La fonction est positive sur donc l'intégrale est positive et est égale à l'aire du domaine hachuré sur la figure.
Sachant que huit petits carreaux ont une aire de .
On compte le nombre de petits carreaux sous la courbe et l'axe des abscisses et délimité par les droites verticales et .
On compte un peu plus de petits carreaux.
Comme petits carreaux ont une aire de , on a donc une aire supérieure à car nous avons petits carreaux.
Autrement dit :
La fonction est positive sur donc l'intégrale est positive et est égale à l'aire du domaine hachuré sur la figure.
Sachant que huit petits carreaux ont une aire de .
On compte le nombre de petits carreaux sous la courbe et l'axe des abscisses et délimité par les droites verticales et .
On compte un peu plus de petits carreaux.
Comme petits carreaux ont une aire de , on a donc une aire supérieure à car nous avons petits carreaux.
Autrement dit :
.