Continuité, dérivation, lectures graphiques et convexité

Exercice 1 - Exercice 1

1 min
0
Cet exercice est un questionnaire à choix multiples.
Pour chaque question posée, une seule des quatre réponses proposées est exacte.
On demande bien sûr de justifier.
Question 1
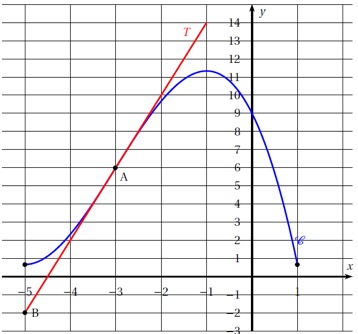
On a représenté dans le repère orthogonal ci-dessous la courbe représentative C\mathscr{C} d'une fonction ff définie et deux fois dérivable sur l'intervalle [−5;1]\left[-5;1\right].
La droite TT est la tangente à la courbe C\mathscr{C} au point A(−3;6)A\left(-3;6\right) et passe par le point (−5;−2)\left(-5;-2\right).
Le point AA est l'unique point d'inflexion de la courbe C\mathscr{C} sur [−5;1]\left[-5;1\right].

On note f′f' la fonction dérivée de la fonction ff.
Alors :
  • f′(−3)=6f'\left(-3\right)=6
  • f′(−3)=4f'\left(-3\right)=4
  • f′(−3)=14f'\left(-3\right)=\frac{1}{4}
  • f′(−3)=16f'\left(-3\right)=\frac{1}{6}

Correction
La bonne réponse est la b.
f′(−3)f'\left(-3\right) correspond au coefficient directeur de la tangente à la courbe au point d'abscisse −3-3 donc au point AA.
De plus, le point BB appartient à cette tangente.
A l'aide du point AA et du point BB on va pouvoir donner le coefficient directeur de la tangente.
f′(−3)=yB−yAxB−xAf'\left(-3\right)=\frac{y_{B} -y_{A} }{x_{B} -x_{A} }
f′(−3)=−2−6−5−(−3)f'\left(-3\right)=\frac{-2-6}{-5-\left(-3\right)}
Ainsi :
f′(−3)=4f'\left(-3\right)=4

Question 2

On note f′′f'' la fonction dérivée seconde de la fonction ff.
Alors :
  • f′′(−3)=6f''\left(-3\right)=6
  • f′′(−3)=4f''\left(-3\right)=4
  • f′′(−3)=0f''\left(-3\right)=0
  • f′′(−3)=14f''\left(-3\right)=\frac{1}{4}

Correction
La bonne réponse est c.
La courbe admet un point d'inflexion en AA d'abscisse −3-3 donc
f′′(−3)=0f''\left(-3\right)=0
Question 3

La fonction ff est :
  • Convexe sur [−5;−3]\left[-5;-3\right]
  • Convexe sur [−5;−1]\left[-5;-1\right]
  • Convexe sur [−3;−1]\left[-3;-1\right]
  • Concave sur [−5;−1]\left[-5;-1\right]

Correction
La bonne réponse est a.
  • Lorsque les tangentes sont situées au-dessus de la courbe sur un intervalle [a,b]\left[a,b\right] alors ff est concave sur [a,b]\left[a,b\right].
  • Lorsque les tangentes sont situées en dessous de la courbe sur un intervalle [a,b]\left[a,b\right] alors ff est convexe sur [a,b]\left[a,b\right].
    On peut également dire que :
  • Lorsque la courbe est située en dessous de ses tangentes sur un intervalle [a,b]\left[a,b\right] alors ff est concave sur [a,b]\left[a,b\right].
  • Lorsque la courbe est située au-dessus de ses tangentes sur un intervalle [a,b]\left[a,b\right] alors ff est convexe sur [a,b]\left[a,b\right].
Sur l'intervalle [−5;−3]\left[-5;-3\right] la courbe est au-dessus de ses tangentes donc ff est convexe sur cet intervalle.
Question 4

La fonction dérivée f′f' est :
  • Décroissante sur [−3;−1]\left[-3;-1\right]
  • Croissante sur [−3;−1]\left[-3;-1\right]
  • Croissante sur [−1;1]\left[-1;1\right]
  • Croissante sur [−5;−1]\left[-5;-1\right]

Correction
La bonne réponse est a.
  • Lorsque les tangentes sont situées au-dessus de la courbe sur un intervalle [a,b]\left[a,b\right] alors ff est concave sur [a,b]\left[a,b\right].
  • Lorsque les tangentes sont situées en dessous de la courbe sur un intervalle [a,b]\left[a,b\right] alors ff est convexe sur [a,b]\left[a,b\right].
    On peut également dire que :
  • Lorsque la courbe est située en dessous de ses tangentes sur un intervalle [a,b]\left[a,b\right] alors ff est concave sur [a,b]\left[a,b\right].
  • Lorsque la courbe est située au-dessus de ses tangentes sur un intervalle [a,b]\left[a,b\right] alors ff est convexe sur [a,b]\left[a,b\right].
Sur l'intervalle [−3;−1]\left[-3;-1\right] la courbe est en-dessous de ses tangentes donc ff est concave sur cet intervalle.
  • Si ff est convexe sur [a;b]\left[a;b\right] alors f′f' est croissante [a;b]\left[a;b\right]
  • Si ff est concave sur [a;b]\left[a;b\right] alors f′f' est décroissante [a;b]\left[a;b\right]
Il en résulte donc que f′f' est décroissante sur [−3;−1]\left[-3;-1\right].
Question 5

Toute primitive FF de la fonction ff est :
  • Décroissante sur [−5;−1]\left[-5;-1\right]
  • Croissante sur [−5;−1]\left[-5;-1\right]
  • Constante sur [−5;−1]\left[-5;-1\right]
  • Décroissante sur [−1;1]\left[-1;1\right]

Correction
La bonne réponse est b.
Une primitive FF de la fonction ff a pour dérivée cette fonction ff.
Il faut donc étudier le signe ff et on obtiendra les variations de FF.
  • Lorsque ff est positive sur [a;b]\left[a;b\right] alors FF est croissante sur [a;b]\left[a;b\right]
  • Lorsque ff est négative sur [a;b]\left[a;b\right] alors FF est décroissante sur [a;b]\left[a;b\right]
ff est positive sur [−5;−1]\left[-5;-1\right] donc la fonction FF est croissante sur cet intervalle.
Question 6

On note I=∫−5−4f(x)dxI=\int _{-5}^{-4}f\left(x\right)dx .
Alors :
  • −2≤I≤0-2\le I\le 0
  • −5≤I≤−4-5\le I\le -4
  • 0<I≤20<I\le 2
  • 2<I<42<I<4

Correction
La bonne réponse est c.
La fonction ff est positive sur [−5;−4]\left[-5;-4\right] donc l'intégrale II est positive et est égale à l'aire du domaine hachuré sur la figure ci-dessous.
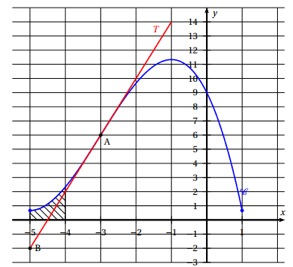On compte le nombre de carreau sous la courbe et l'axe des abscisses délimité par les droites verticales x=−4x=-4 et x=−5x=-5.
Sachant que chaque carreau a une aire de 11, on dénombre qu'il y a un carreau plein hachuré et un deuxième pas complet.
Il en résulte donc que :
0<I≤20<I\le 2