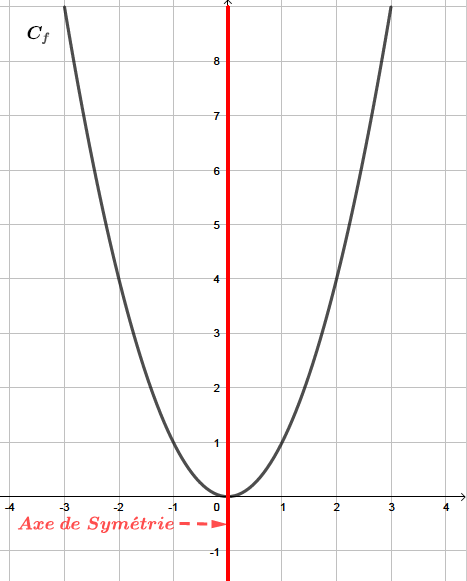
Variations et extremums des fonctions. Lecture graphique . Fonctions paires et impaires
Savoir démontrer qu'une fonction est paire - Exercice 1
5 min
10
Question 1
Soit définie sur par . Démontrer que la fonction est paire.
Correction
Soit est une fonction définie sur un intervalle . On dit que la fonction est paire si les deux conditions ci-dessous sont vérifiées :
- ère condition : pour tout réel appartenant à , le réel appartient à .
- ème condition : pour tout réel appartenant à ,
Donc pour tout réel appartenant à son opposé appartient également à l'intervalle . La ère condition est vérifiée.
Pour tout réel appartenant à , on a :
Soit :
Donc est une fonction paire.