Probabilités
Loi de probabilité - Exercice 1
10 min
15
On lance un dé pipé. Les probabilités d’apparition des faces vérifient : ; ;
On suppose que le lancer est régie par une loi de probabilité.
On suppose que le lancer est régie par une loi de probabilité.
Question 1
Dresser la loi de probabilité du lancer de ce dé pipé. Calculer alors la probabilité
Correction
La loi de probabilité est donnée ci-dessous :
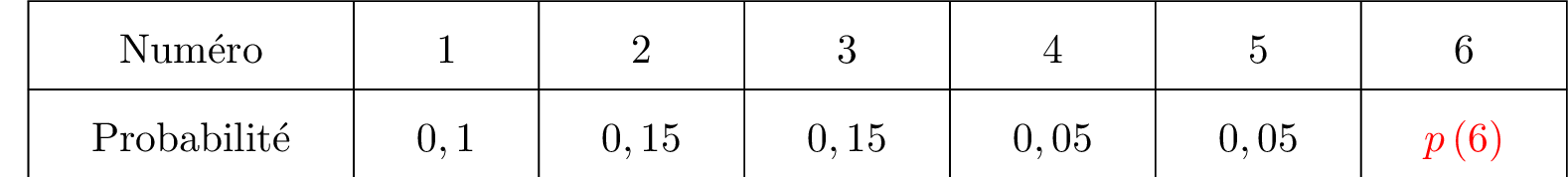 Or, nous savons que :
Or, nous savons que :
équivaut successivement à :
Finalement, la loi de probabilité est :
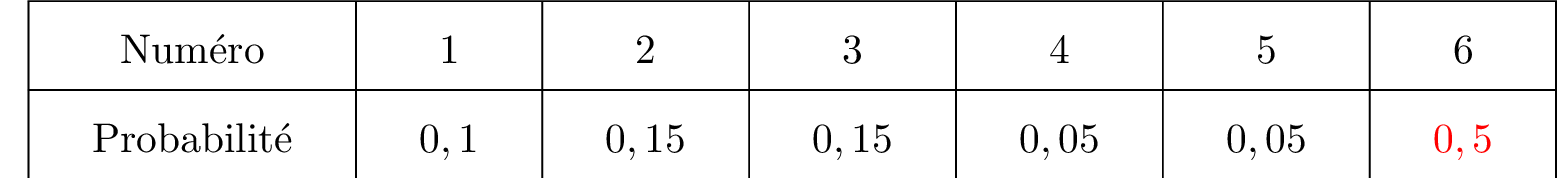
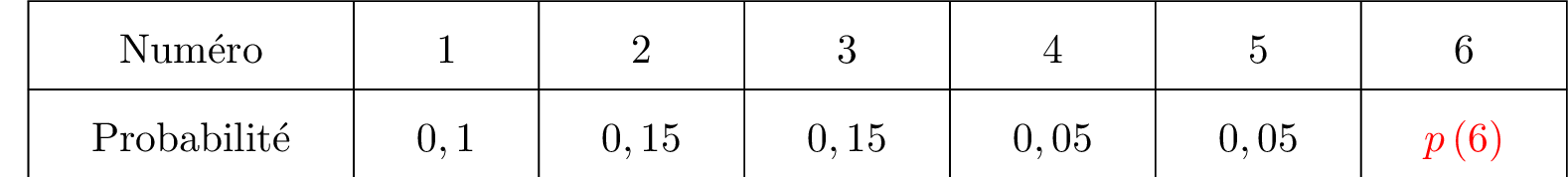
équivaut successivement à :
Finalement, la loi de probabilité est :
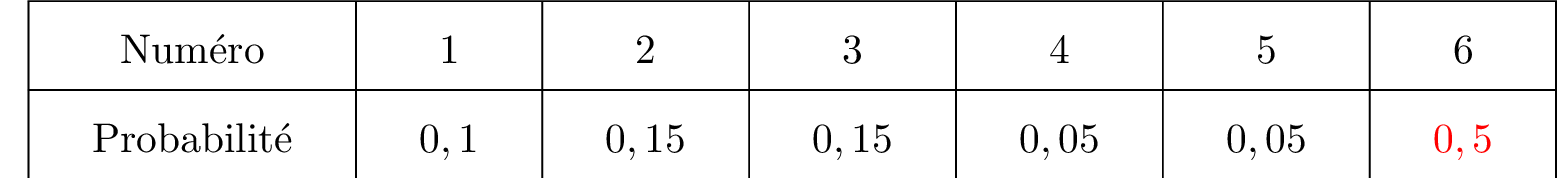
Question 2
On note les événements :
: "le numéro est pair"
: "le numéro est strictement supérieur à "
: "le numéro est pair"
: "le numéro est strictement supérieur à "
Calculer
Correction
Pour tous évènements et , on a :
Enfin :
correspond à choisir un numéro pair et un numéro strictement supérieur à . Autrement dit, cela revient à choisir le numéro .
Ainsi :
Finalement :
équivaut successivement à :