Premières notions sur les suites numériques
Etudier les variations d'une suite à l'aide de la fonction associée - Exercice 1
25 min
40
Question 1
Pour tout entier naturel , on donne la suite définie par : . Etudiez les variations de la suite .
Correction
Soit une fonction définie sur et une suite numérique définie sur par . Soit un entier naturel.
Dans ce corrigé, nous n'allons pas utiliser la méthode de l'étude du signe de . Nous allons utiliser une fonction associée.- Si est croissante sur l'intervalle alors la suite est croissante à partir du rang .
- Si est décroissante sur l'intervalle alors la suite est décroissante à partir du rang .
On considère la fonction associée définie sur par : .
Nous avons donc bien .
Etudions les variations de sur .
On reconnaît la forme avec
Ainsi : .
Il vient alors que :
Pour tout réel , on vérifie aisément que et que .
Il en résulte donc que pour tout réel , on a .
Donc est décroissante sur . On en déduit donc que la suite est décroissante.
Question 2
Pour tout entier naturel , on donne la suite définie par : . Etudiez les variations de la suite .
Correction
Soit une fonction définie sur et une suite numérique définie sur par . Soit un entier naturel.
Dans ce corrigé, nous n'allons pas utiliser la méthode de l'étude du signe de . Nous allons utiliser une fonction associée.- Si est croissante sur l'intervalle alors la suite est croissante à partir du rang .
- Si est décroissante sur l'intervalle alors la suite est décroissante à partir du rang .
On considère la fonction associée définie sur par : .
Nous avons donc bien .
Etudions les variations de sur .
Pour tout réel , on vérifie aisément que et que ce qui signifie donc que .
Il en résulte donc que pour tout réel , on a .
Donc est croissante sur . On en déduit donc que la suite est croissante.
Question 3
Pour tout entier naturel , on donne la suite définie par : . Etudiez les variations de la suite .
Correction
Soit une fonction définie sur et une suite numérique définie sur par . Soit un entier naturel.
Dans ce corrigé, nous n'allons pas utiliser la méthode de l'étude du signe de . Nous allons utiliser une fonction associée.- Si est croissante sur l'intervalle alors la suite est croissante à partir du rang .
- Si est décroissante sur l'intervalle alors la suite est décroissante à partir du rang .
On considère la fonction associée définie sur par : .
Nous avons donc bien .
Etudions les variations de sur .
Pour tout réel , on vérifie aisément que et que .
Il en résulte donc que pour tout réel , on a .
Donc est décroissante sur . On en déduit donc que la suite est décroissante.
Question 4
Pour tout entier naturel , on donne la suite définie par : . Etudiez les variations de la suite .
Correction
Soit une fonction définie sur et une suite numérique définie sur par . Soit un entier naturel.
Dans ce corrigé, nous n'allons pas utiliser la méthode de l'étude du signe de . Nous allons utiliser une fonction associée.- Si est croissante sur l'intervalle alors la suite est croissante à partir du rang .
- Si est décroissante sur l'intervalle alors la suite est décroissante à partir du rang .
On considère la fonction associée définie sur par : .
Nous avons donc bien .
Etudions les variations de sur .
Il nous faut étudier le signe de sur l'intervalle
Ainsi :
Il en résulte donc que :
Pour tout réel , on a .
Pour tout réel , on a .
Nous traduisons cela dans un tableau de variation :
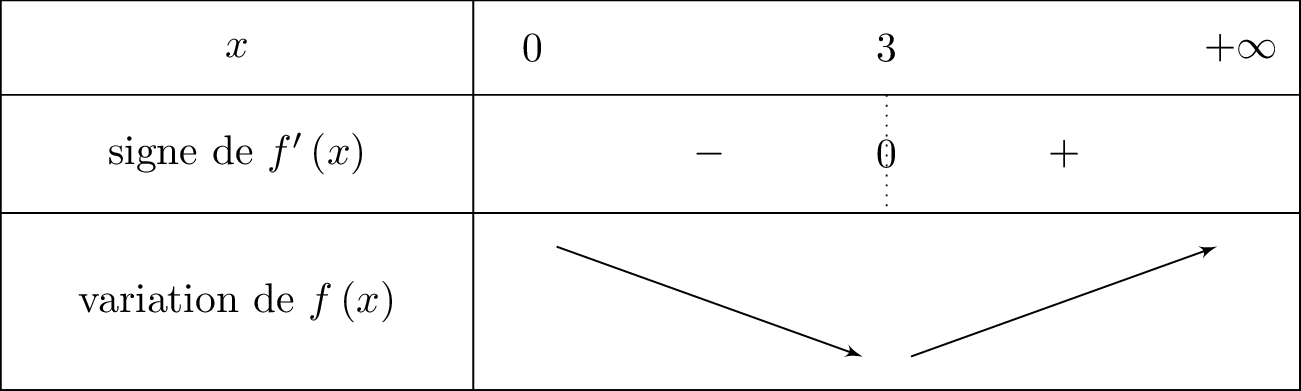
Question 5
Pour tout entier naturel non nul , on donne la suite définie par : . Etudiez les variations de la suite .
Correction
N'oublions pas ici que .
Dans ce corrigé, nous n'allons pas utiliser la méthode de l'étude du signe de . Nous allons utiliser une fonction associée.
On considère la fonction associée définie sur par : . Nous avons donc bien .
Etudions les variations de sur .
On reconnaît la forme avec et
Ainsi : et .
Il vient alors que :
Ainsi :
Or et donc . Le signe de dépend alors du signe de .
Cela signifie que pour tout réel , nous allons avoir .
Nous traduisons cela dans un tableau de variation que l'on donne ci-dessous :
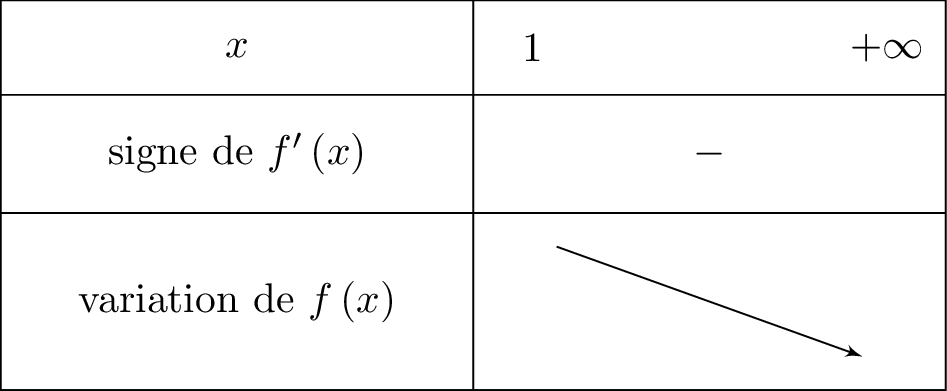
Dans ce corrigé, nous n'allons pas utiliser la méthode de l'étude du signe de . Nous allons utiliser une fonction associée.
On considère la fonction associée définie sur par : . Nous avons donc bien .
Etudions les variations de sur .
On reconnaît la forme avec et
Ainsi : et .
Il vient alors que :
Ainsi :
Or et donc . Le signe de dépend alors du signe de .
Cela signifie que pour tout réel , nous allons avoir .
Nous traduisons cela dans un tableau de variation que l'on donne ci-dessous :

Soit une fonction définie sur et une suite numérique définie sur par . Soit un entier naturel.
On en déduit donc que la suite est décroissante à partir du rang .- Si est croissante sur l'intervalle alors la suite est croissante à partir du rang .
- Si est décroissante sur l'intervalle alors la suite est décroissante à partir du rang .
Question 6
Pour tout entier naturel , on donne la suite définie par : . Etudiez les variations de la suite .
Correction
On considère la fonction associée définie sur par : . Nous avons donc bien .
On reconnait une fonction du second degré ( forme canonique ). Nous pouvons donc dresser rapidement le tableau de variation de .
Nous identifions ; et .
On reconnait une fonction du second degré ( forme canonique ). Nous pouvons donc dresser rapidement le tableau de variation de .
Nous identifions ; et .

Soit une fonction définie sur et une suite numérique définie sur par . Soit un entier naturel.
On en déduit donc que la suite est croissante à partir du rang .- Si est croissante sur l'intervalle alors la suite est croissante à partir du rang .
- Si est décroissante sur l'intervalle alors la suite est décroissante à partir du rang .