Dérivation
Exercices types : ème partie - Exercice 1
12 min
30
Soit une fonction définie sur par où , et sont des réels. est sa courbe représentative dans un repère .
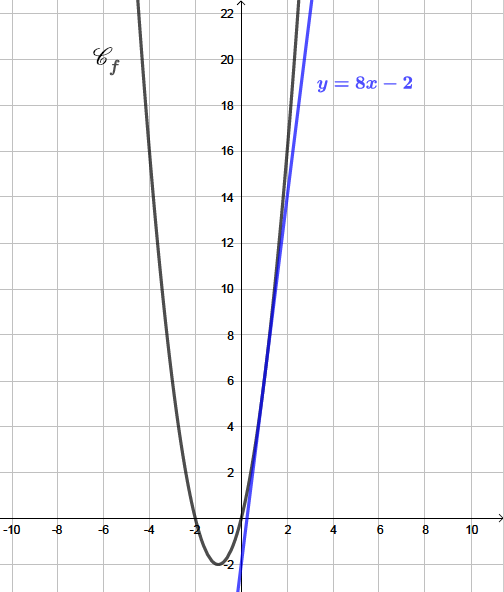
Nous savons que passe par l'origine du repère et que la droite d'équation est tangente à au point d'abscisse .
Nous savons que passe par l'origine du repère et que la droite d'équation est tangente à au point d'abscisse .
Question 1
Déterminer le réel .
Correction
Nous savons que passe par l'origine du repère ce qui signifie que .
Il vient alors que :
Ce qui donne :
Il vient alors que :
Ce qui donne :
Question 2
Déterminer les coordonnées du point .
Correction
La droite d'équation est tangente à au point d'abscisse . Cela signifie qu'au point la droite et la courbe sont confondues. C'est à dire que le point appartient à la droite et à la courbe .
L'abscisse du point est et comme le point appartient à la droite alors on peut écrire que :
Les coordonnées du point sont alors :
L'abscisse du point est et comme le point appartient à la droite alors on peut écrire que :
Les coordonnées du point sont alors :
Question 3
En déduire les réels et .
Correction
D'après la question précédente, nous savons que les coordonnées du point sont .
Nous pouvons donc écrire que
Ce qui se traduit par :
et comme d'après la question alors :
De plus, la droite d'équation est tangente à la courbe au point d'abscisse . Cela se traduit par .
En effet, le coefficient directeur de la tangente au point d'abscisse correspond au nombre dérivée.
Comme alors :
d'où
Or va donc permettre d'écrire que c'est à dire :
Nous avons donc un système deux équations à deux inconnues . Nous allons résoudre le système à l'aide de la méthode par substitution. Pour cela, on cherche une inconnue dont le coefficient vaut . Ici, à la première ligne du système nous avons . Nous allons donc exprimer en fonction de . Il vient alors que :
. Nous allons maintenant remplacer par dans la deuxième ligne .
. Maintenant, nous connaissons la valeur de , il suffit de remplacer dans la première ligne le par . Il vient :
Le couple solution du système est alors :
Nous connaissons maintenant les valeurs de , et . Nous pouvons donc écrire que :
Nous pouvons donc écrire que
Ce qui se traduit par :
et comme d'après la question alors :
De plus, la droite d'équation est tangente à la courbe au point d'abscisse . Cela se traduit par .
En effet, le coefficient directeur de la tangente au point d'abscisse correspond au nombre dérivée.
Comme alors :
d'où
Or va donc permettre d'écrire que c'est à dire :
Nous avons donc un système deux équations à deux inconnues . Nous allons résoudre le système à l'aide de la méthode par substitution. Pour cela, on cherche une inconnue dont le coefficient vaut . Ici, à la première ligne du système nous avons . Nous allons donc exprimer en fonction de . Il vient alors que :
. Nous allons maintenant remplacer par dans la deuxième ligne .
. Maintenant, nous connaissons la valeur de , il suffit de remplacer dans la première ligne le par . Il vient :
Le couple solution du système est alors :
Nous connaissons maintenant les valeurs de , et . Nous pouvons donc écrire que :
